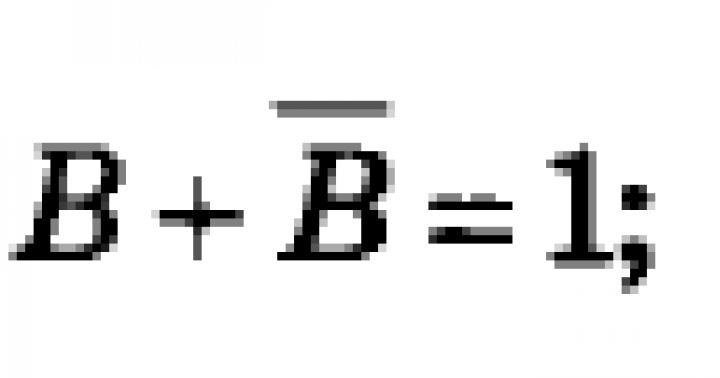Prawa de Morgana w teorii mnogości. Twierdzenia o absorpcji, klejeniu i de morgana

Twierdzenie o absorpcji napisane w dwóch formach - dysjunktywnej i

spojówkowy, odpowiednio:

A + AB \u003d A (16)

A(A + B)=A (17)

Udowodnijmy pierwsze twierdzenie. Wyjmijmy literę A z nawiasów:

A + AB \u003d A (1 + B)

Zgodnie z twierdzeniem (3) 1 + B = 1, zatem

A(1 + B) = A 1 = A

Aby udowodnić drugie twierdzenie, rozszerzamy nawiasy:

A(A + B) = A A + AB = A + AB

Rezultatem jest wyrażenie, które właśnie zostało udowodnione.

Rozważmy kilka przykładów zastosowania twierdzenia o absorpcji dla

uproszczenie formuł logicznych.

Twierdzenie o klejeniu ma również dwie formy - dysjunktywną i

spojówka:

Udowodnijmy pierwsze twierdzenie:

ponieważ zgodnie z twierdzeniami (5) i (4)

Aby udowodnić drugie twierdzenie, otwieramy nawiasy:

Zgodnie z twierdzeniem (6) zatem:

Zgodnie z twierdzeniem o absorpcji (16) A + AB \u003d A

Twierdzenie o absorpcji, podobnie jak twierdzenie o klejeniu, jest stosowane podczas upraszczania

formuły logiczne, na przykład:

Twierdzenie de Morganałączy wszystkie trzy podstawowe operacje algebry Boole'a

Dyfuzja, koniunkcja i inwersja:

Pierwsze twierdzenie brzmi następująco: odwrócenie koniunkcji jest alternatywą

inwersje. Po drugie, inwersja alternatywy jest koniunkcją inwersji. Możesz udowodnić twierdzenia Morgana za pomocą tabel prawdy dla lewej i prawej strony.

Twierdzenie De Morgana odnosi się również do większej liczby zmiennych:

Wykład 5

Odwracanie wyrażeń złożonych

Twierdzenie de Morgana dotyczy nie tylko pojedynczych spójników

lub alternatywy, ale także do bardziej złożonych wyrażeń.

Znajdźmy odwrotność wyrażenia AB + CD , reprezentowana jako alternatywa spójników. Inwersja zostanie uznana za zakończoną, jeśli znaki ujemne znajdują się tylko nad zmiennymi. Wprowadźmy notację: AB = X;

CD=Y następnie

Znajdź i zastąp wyrażenie (22):

W ten sposób:

Rozważ wyrażenie przedstawione w formie łączącej:

(A + B) (C + D)

Znajdźmy jego inwersję w postaci

Wprowadźmy notację: A + B = X; C + D \u003d Y, następnie

Znajdź i zastąp je wyrażeniem

W ten sposób:

Podczas odwracania złożonych wyrażeń możesz użyć następującej reguły. Aby znaleźć inwersję, należy zastąpić znaki koniunkcji znakami alternatywy, a znaki alternatywy znakami koniunkcji, a nad każdą zmienną umieścić inwersję:

Pojęcie funkcji Boole'a

V w ogólnym przypadku funkcję (łac. functio - wydajność, zgodność,

mapowanie) to pewna zasada (prawo), zgodnie z którą każdy element zbioru x, który jest zakresem zmiennej niezależnej X, przypisywany jest pewien element zestawu F,

co rozumiane jest jako zakres wartości zmiennej zależnej F . W przypadku funkcji logicznych X=F = (0,1). Regułą, według której określa się funkcję, może być dowolna formuła logiczna, na przykład:

Symbol F oto funkcja, która podobnie jak argumenty A, PNE, zmienna binarna.

Argumenty są zmiennymi niezależnymi, mogą przyjmować dowolną wartość - 0 lub 1. Funkcja F - zmienna zależna. Jego znaczenie jest całkowicie określone przez wartości zmiennych i logiczne powiązania między nimi.

Główną cechą funkcji jest to, że aby określić jej wartość, w ogólnym przypadku konieczne jest poznanie wartości wszystkich argumentów, od których zależy. Na przykład powyższa funkcja zależy od trzech argumentów A, VS. Jeśli weźmiemy A = 1, to otrzymamy

tj. otrzymuje się nowe wyrażenie, nierówne ani zero, ani

jednostka. Niech teraz V= 1. Wtedy

tj. w tym przypadku nie wiadomo, czy funkcja jest równa zero czy jeden.

Na koniec weźmy Z= 0. Wtedy otrzymujemy: F = 0. Tak więc, jeśli w pierwotnym wyrażeniu przyjmiemy A = 1, V= 1, Z = 0, wtedy funkcja przyjmie wartość zerową: f= 0.

Rozważać pojęcie zbioru wartości zmiennych .

Jeśli wszystkim argumentom, od których zależy funkcja, przypisano określone wartości, to mówi się o zestawie wartości argumentów, które mogą być

po prostu nazwij to zestawem. Zestaw wartości argumentów to ciąg zer i jedynek, na przykład 110, gdzie pierwsza cyfra odpowiada pierwszemu argumentowi, druga drugiemu, a trzecia trzeciemu. Oczywiście trzeba z góry uzgodnić, co to jest pierwszy, drugi czy, powiedzmy, piąty argument. Aby to zrobić, wygodnie jest użyć alfabetycznego układu liter.

Na przykład, jeśli

wtedy według alfabetu łacińskiego pierwszym argumentem jest R, druga -

Q, trzecia - x, po czwarte - U. Wtedy przy zestawie wartości argumentów jest to łatwe

znajdź wartość funkcji. Niech zostanie podany np. zbiór 1001. Według jego

rekordów, czyli w zbiorze 1001 dana funkcja jest równa jeden.

Zwróć uwagę, że zestaw wartości argumentów to zestaw

zera i jedynek. Liczby binarne to także zestawy zer i jedynek.

Rodzi to pytanie - czy zbiory można uznać za binarne?

liczby? Jest to możliwe, a w wielu przypadkach bardzo wygodne, zwłaszcza jeśli binarny

przekonwertować liczbę na dziesiętną. Na przykład, jeśli

A = 0, B = 1, C = 1, D = 0,

0 * 2 3 +1 * 2 2 +1 * 2 1 +0 * 2 0 = 4+2 = 6

tzn. dany zbiór ma liczbę 6 w postaci dziesiętnej.

Jeśli chcesz znaleźć wartości argumentów według liczby dziesiętnej, to

postępujemy w odwrotnej kolejności: najpierw tłumaczymy liczbę dziesiętną na binarną, następnie dodajemy tyle zer po lewej stronie, aby łączna liczba cyfr była równa liczbie argumentów, po czym znajdujemy wartości argumentów.

Niech na przykład wymagane jest znalezienie wartości argumentów A, B, C, D, E, F przez zbiór z liczbą 23. Liczbę 23 zamieniamy na system dwójkowy metodą

dzieląc przez dwa:

W rezultacie otrzymujemy 23 10 = 10111 2 . Jest to liczba pięciocyfrowa, a w sumie

jest sześć argumentów, dlatego po lewej stronie musi być napisane jedno zero:

23 10 = 010111 2 . Stąd znajdujemy:

A = 0, B = 1, C = 0, D = 1, E = 1, F = 1.

Ile jest zestawów, jeśli liczba jest znana? P argumenty? Oczywiście, aż jest n-bitowych liczb binarnych, czyli 2 n

Wykład 6

Ustawianie funkcji logicznej

Jeden sposób już znamy. Jest analityczny, czyli w postaci wyrażenia matematycznego wykorzystującego zmienne binarne i operacje logiczne. Oprócz tego istnieją inne sposoby, z których najważniejszy jest tabelaryczny. W tabeli wymieniono wszystkie możliwe zestawy wartości argumentów, a dla każdego zestawu wskazana jest wartość funkcji. Taka tabela nazywana jest tabelą korespondencji (prawdy).

Na przykładzie funkcji

Zastanówmy się, jak zbudować dla niego tabelę przeglądową.

Funkcja zależy od trzech argumentów A, B, C. Dlatego w tabeli

podajemy trzy kolumny na argumenty A,B,C i jedną kolumnę na wartości funkcji f. Na lewo od kolumny A warto umieścić kolejną kolumnę. Zapiszemy w nim liczby dziesiętne, które odpowiadają zestawom, jeśli uznamy je za trzycyfrowe liczby binarne. Ten dziesiętny

kolumna została wprowadzona dla wygody pracy ze stołem, dlatego w zasadzie

można to zaniedbać.

Wypełniamy tabelę. Wiersz z numerem LLC brzmi:

A = B = C = 0.

Zdefiniujmy wartość funkcji na tym zestawie:

W kolumnie f wpisujemy zero w wierszu ze zbiorem 000.

Kolejny zestaw: 001, czyli e. A = B = 0, C = 1. Znajdź wartość funkcji

na tym zestawie:

W zestawie 001 funkcja jest równa 1, dlatego w kolumnie f w wierszu z

numer 001 zapisujemy jednostkę.

Podobnie obliczamy wartości funkcji na wszystkich pozostałych zbiorach i

uzupełnij całą tabelę.

Łączność

x 1 (x 2 x 3) \u003d (x 1 x 2) x 3;

x 1 Ú (x 2 Ú x 3) \u003d (x 1 Ú x 2) Ú x 3.

przemienność

x 1 x 2 = x 2 x 1

x 1 Ú x 2 = x 2 Ú x 1

Dystrybucja koniunkcji względem alternatywy

x 1 (x 2 Ú x 3) \u003d x 1 x 2 Ú x 1 x 3.

Dystrybucja alternatywy względem koniunkcji

x 1 (x 2 × x 3) = (x 1 Úx 2) × (x 1 Úx 3). *

Idempotencja (tautologia)

dwa razy nie

Stałe właściwości

x i 1 = x; (prawa zbioru uniwersalnego)

x i 0 = 0; (prawa zerowe)

Zasady (prawa) de Morgan

Prawo sprzeczności (dodatkowość)

Prawo wyłączenia środka (dodatkowe)

Dowody tych wszystkich formuł są trywialne. Jedną z opcji jest zbudowanie tabel prawdy z lewej i prawej części i porównanie ich.

Zasady klejenia

Reguła sklejania dla elementarnych spójników wynika z prawa rozdzielczego, prawa komplementarności i prawa zbioru uniwersalnego: alternatywę dwóch sąsiednich spójników można zastąpić jednym spójnikiem elementarnym, który jest wspólną częścią oryginalnych spójników .

Zasada sklejania dla sum elementarnych wynika z prawa rozdzielczego drugiego rodzaju, prawa komplementarności i prawa zbioru zerowego: połączenie dwóch sąsiednich alternatyw może być zastąpione przez jedną elementarną alternatywę, która jest wspólną częścią oryginalnych alternatyw .

Zasada absorpcji

Reguła absorpcji dla sumy dwóch iloczynów elementarnych wynika z prawa rozdzielności pierwszego rodzaju oraz praw zbioru uniwersalnego: alternatywę dwóch elementarnych koniunkcji, z których jeden jest składnikiem drugiego, można zastąpić koniunkcją z mniejszą liczbą operandów .

Reguła absorpcji dla iloczynu sum elementarnych wynika z prawa rozdzielności drugiego rodzaju oraz praw zbioru zerowego: połączenie dwóch elementarnych alternatyw, z których jeden jest składnikiem drugiego, może być zastąpiony przez elementarną alternatywę mającą mniej argumentów.

Reguła wdrażania

Ta zasada określa odwrotne działanie klejenia.

Zasada rozwinięcia iloczynu elementarnego do logicznej sumy iloczynów elementarnych wyższego rzędu (w granicy do r = n, czyli do składowych jedności, o czym będzie mowa niżej) wynika z praw zbioru uniwersalnego , prawo dystrybucji pierwszego rodzaju i odbywa się w trzech etapach:

W opracowywanym iloczynie elementarnym rangi r, jednostki n-r wprowadza się jako czynniki, gdzie n jest rangą składnika jednostki;

Każda jednostka zostaje zastąpiona przez sumę logiczną jakiejś zmiennej nieobecnej w pierwotnym iloczynie elementarnym i jego negację: x ja v `x ja = 1;

Wszystkie nawiasy są rozszerzane na podstawie prawa rozdzielczego pierwszego rodzaju, które prowadzi do rozwinięcia pierwotnego iloczynu elementarnego rzędu r na sumę logiczną 2 n-r składowych jednostkowych.

Elementarna reguła rozwinięcia iloczynu służy do minimalizacji funkcji algebry logicznej (FAL).

Reguła rozwinięcia sumy elementarnej rangi r do iloczynu sum elementarnych rangi n (składającej się z zera) wynika z praw zbioru zer (6) i prawa rozdzielności drugiego rodzaju (14) i jest wykonywane w trzech etapach:

W rozszerzonej sumie rang r, n-r zer są wprowadzone jako terminy;

Każde zero jest reprezentowane jako logiczny iloczyn jakiejś zmiennej nieobecnej w początkowej sumie i jej negacji: x ja·` x ja = 0;

Otrzymane wyrażenie jest przekształcane na podstawie prawa rozdzielności drugiego rodzaju (14) w taki sposób, że początkowa suma rang rozwija się w logiczny iloczyn 2 n-r zerowych składników.

16. Pojęcie kompletnego systemu. Przykłady kompletnych systemów (z dowodem)

Definicja. Zbiór funkcji algebry logicznej A nazywamy systemem zupełnym (w P2), jeśli dowolna funkcja algebry logicznej może być wyrażona przez formułę nad A.

Układ funkcji A=( f 1 , f 1 ,…, f m) który jest kompletny nazywa się podstawa.

Minimalna podstawa to taka podstawa, dla której usunięcie przynajmniej jednej funkcji f1, który stanowi tę podstawę, przekształca system funkcji (f 1 , f 1 ,…, f m) w niekompletnym.

Twierdzenie. Układ A = (∨, &, ) jest kompletny.

Dowód. Jeśli funkcja algebry logicznej f nie jest identycznie zerem, to f jest wyrażone jako doskonała dysjunktywna forma normalna, która zawiera tylko alternatywę, koniunkcję i negację. Jeśli f ≡ 0, to f = x & x . Twierdzenie zostało udowodnione.

Lemat. Jeżeli system A jest zupełny i dowolna funkcja systemu A może być wyrażona za pomocą wzoru względem jakiegoś innego systemu B, to B jest również systemem zupełnym.

Dowód. Rozważ dowolną funkcję algebry logicznej f (x 1 , …, x n) i dwa układy funkcji: A = (g 1 , g 2 , …) i B = (h 1 , h 2 , …). Ze względu na to, że system A jest kompletny, funkcję f można wyrazić jako formułę nad nim:

f (x 1 , …, x n) = ℑ

gdzie g i = ℜ i

czyli funkcja f jest reprezentowana jako

f (x 1 , …, x n)=ℑ[ℜ1,ℜ2,...]

innymi słowy, może być reprezentowana przez formułę nad B. Wyliczając w ten sposób wszystkie funkcje algebry logiki, otrzymujemy, że system B również jest zupełny. Lemat jest udowodniony.

Twierdzenie. Następujące systemy są kompletne w P 2:

4) (&, ⊕ , 1) podstawa Zhegalkina.

Dowód.

1) Wiadomo (Twierdzenie 3), że układ A = (&, V, ) jest kompletny. Pokażmy, że system B = ( V, . Rzeczywiście, z prawa de Morgana (x& y) = (x ∨ y) otrzymujemy, że x & y = (x ∨ y) , tj. koniunkcja jest wyrażona przez alternatywę i negacja, a wszystkie funkcje systemu A są wyrażone przez formuły nad systemem B. Zgodnie z lematem system B jest zupełny.

2) Podobnie do pozycji 1: (x ∨ y) = x & y ⇔ x ∨ y =(x & y) a Lemat 2 implikuje prawdziwość pozycji 2.

3) x | y=(x&y), x | x = x; x i y = (x | y) = (x | y) | (x | y) i zgodnie z Lematem 2 system jest kompletny.

4) x = x ⊕1 i zgodnie z Lematem 2 system jest kompletny.

Twierdzenie zostało udowodnione.

17. Algebra Żegalkina. Właściwości operacyjne i kompletność

Zbiór funkcji logicznych zdefiniowanych w bazie Zhegalkina S4=(⊕,&,1) nazywa się Algebra Zhegalkina.

Podstawowe właściwości.

1. przemienność

h1⊕h2=h2⊕h1 h1&h2=h2&h1

2. stowarzyszenie

h1⊕(h2⊕h3)=(h1⊕h2)⊕h3 h1&(h2&h3)=(h1&h2)&h3

3. dystrybucyjność

h1&(h2⊕h3)=(h1&h2)⊕(h1&h3)

4. stałe właściwości

5. h⊕h=0 h&h=h
Oświadczenie. Poprzez operacje algebry Zhegalkina można wyrazić wszystkie inne funkcje logiczne:

x→y=1⊕x⊕xy

x↓y=1⊕x⊕y⊕xy

18. Wielomian Żegalkina. Metody budowy. Przykład.

Wielomian Zhegalkina (wielomian modulo 2) z n zmienne x 1 ,x 2 ... x n nazywamy wyrażeniem postaci:

c 0 ⊕c 1 x 1 ⊕c 2 x 2 ⊕ ... ⊕c n x n ⊕c 12 x 1 x 2 ⊕ ... ⊕c 12 ... n x 1 x 2 ... x n ,

gdzie stałe C k mogą przyjmować wartości 0 lub 1.

Jeśli wielomian Zhegalkina nie zawiera iloczynów poszczególnych zmiennych, nazywa się to liniową (funkcją liniową).

Na przykład f=x⊕yz⊕xyz i f 1 =1⊕x⊕y⊕z są wielomianami, przy czym ten ostatni jest funkcją liniową.

Twierdzenie. Każda funkcja Boole'a jest reprezentowana jako wielomian Zhegalkina w unikalny sposób.

Przedstawimy główne metody konstruowania wielomianów Zhegalkina danej funkcji.

1. Metoda współczynników nieokreślonych. Niech P(x 1 ,x 2 ... x n) będzie wymaganym wielomianem Zhegalkina realizującym daną funkcję f(x 1 ,x 2 ... x n). Piszemy to w formie

P=c 0 ⊕c 1 x 1 ⊕c 2 x 2 ⊕ ... ⊕c n x n ⊕c 12 x 1 x 2 ⊕ ... ⊕c 12 ... n x 1 x 2 ... x n

Znajdźmy współczynniki C k . Aby to zrobić, podajemy kolejno zmienne x 1 ,x 2 ... x n wartości z każdego wiersza tabeli prawdy. W rezultacie otrzymujemy układ 2 n równań z 2 n niewiadomymi, który ma unikalne rozwiązanie. Rozwiązując go, znajdujemy współczynniki wielomianu P(X 1 ,X 2 ... X n).

2. Metoda oparta na przekształceniu formuł na zbiorze spójników (,&). Zbuduj jakąś formułę F nad zbiorem powiązań (,&) realizujących daną funkcję f(X 1 ,X 2 ... X n). Następnie zamieniamy wszędzie podformuły postaci A na A⊕1, otwieramy nawiasy za pomocą prawa rozdzielności (patrz własność 3), a następnie stosujemy własności 4 i 5.

Przykład. Skonstruuj wielomian Zhegalkina funkcji f(X,Y)=X→Y

Rozwiązanie.
1. (metoda niepewnych współczynników). Wymagany wielomian zapisujemy w postaci:

P=c 0 ⊕c 1 x⊕c 2 y⊕c 12 xy

Korzystając z tabeli prawdy implikacji, otrzymujemy to

f(0,0)=P(0,0)=C 0 =1

f(0,1)=P(0,1)=C 0 ⊕C 2 =1

f(1,0)=P(1,0)=C 0 ⊕C 1 =0

f(1,1)=P(1,1)=C 0 C 1 ⊕C 2 ⊕C 12 =1

Skąd kolejno znajdujemy, C 0 =1, C 1 =1, C 2 =0, C 12 =1

Zatem: x→y=1⊕X⊕XY.

2. (Sposób przeliczania formuł.). Mamy: x→y=xvy=(xy)=(x(y⊕1)) ⊕1=1⊕x⊕xy
Zauważ, że zaletą algebry Zhegalkina (w porównaniu z innymi algebrami) jest arytmetyzacja logiki, która umożliwia przeprowadzanie transformacji funkcji Boole'a w dość prosty sposób. Jego wadą w porównaniu z algebrą Boole'a jest uciążliwość formuł.

Podobne informacje.

Rozważane operacje na zbiorach podlegają pewnym prawom, które przypominają dobrze znane elementarne prawa algebry liczb. To definiuje nazwę ustawić algebrę, która jest często nazywana algebrą zbiorów Boole'a, co jest związane z nazwiskiem angielskiego matematyka Johna Boole'a, który swoje badania logiczne oparł na idei analogii między algebrą a logiką.

Dla dowolnych zbiorów A, B i C prawdziwe są następujące tożsamości (tabela 3.1):

Tabela 3.1

1. Prawo tożsamości
2. Przemienność związku	2'. Przemienność skrzyżowania
3. Zrzeszenie się związku	3'. Powiązanie skrzyżowania
4. Rozdzielczość związku względem skrzyżowania	4'. Dystrybucja skrzyżowania w stosunku do związku
5. Prawa działania z pustym i uniwersalne zestawy U (prawo wyłączonego środka)	5'. Prawa działania z pustym i uniwersalne zestawy U (prawo sprzeczności)
6. Prawo idempotentności stowarzyszenia	6'. Prawo idempotentności przecięcia
7. Prawo De Morgana	7'. Prawo de Morgana
8. Prawo eliminacji (absorpcji)	osiem'. Prawo eliminacji (absorpcji)
9. Prawo sklejania	9'. Prawo więzi
10. Prawo Poreckiego	10 minut. Prawo Poreckiego
11. Prawo inwolucji (podwójne uzupełnienie)

Prawa algebry zbiorów w odniesieniu do operacji przecięcia () i sumy () podlegają zasadzie dwoistości: jeśli w jakimkolwiek prawie wszystkie znaki przecięcia są zastąpione znakami sumy, a wszystkie znaki sumy są znakami przecięcia , znak wszechświata (U) zostaje zastąpiony znakiem pustego zbioru (Ø), a znak pustego - znakiem wszechświata, wtedy znowu otrzymujemy poprawną tożsamość. Na przykład (na mocy tej zasady) wynika z itp.

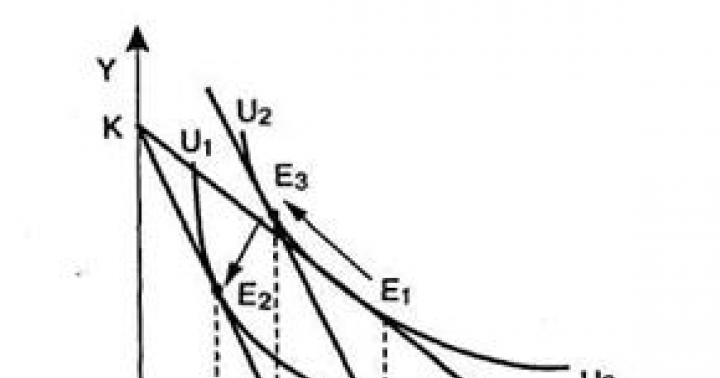
3.1. Sprawdzanie prawdziwości tożsamości za pomocą diagramów Eulera-Venna

Wszystkie prawa algebry zbiorów można przedstawić wizualnie i udowodnić za pomocą diagramów Eulera-Venna. Do tego potrzebujesz:

Narysuj odpowiedni diagram i zaciemnij wszystkie zestawy po lewej stronie równania.

Narysuj kolejny diagram i zrób to samo dla prawej strony równania.

Ta tożsamość jest prawdziwa wtedy i tylko wtedy, gdy ten sam obszar jest zacieniony na obu diagramach.

Uwaga 3.1. Dwa przecinające się okręgi dzielą cały zbiór uniwersalny na cztery regiony (patrz ryc. 3.1)

Uwaga 3.2. Trzy przecinające się okręgi dzielą cały uniwersalny zbiór na osiem regionów (patrz rys. 3.2):

Uwaga 3.2. Pisząc warunki różnych przykładów, często używa się notacji:

 - z ... wynika z ...;

 - wtedy i tylko wtedy, gdy...

Zadanie 3.1 . Uprość wyrażenia algebry zestawów:

Rozwiązanie.

Zadanie 3 .2 . Udowodnij tożsamości:

(AB)\B = A\B;

A(BC) = A\(A\B)(A\C).

Rozwiązanie.

Zadanie 3.3 . Udowodnij następujące relacje na dwa sposoby: za pomocą diagramów i za pomocą definicji równości zbiorów.

Rozwiązanie.

2. Dowód za pomocą definicji równości zbiorów.

Z definicji zbiory X i Y są równe, jeśli jednocześnie spełnione są następujące relacje: XY i YX.

Pokażmy najpierw, że
. Pozwalać x jest dowolnym elementem zbioru
, to jest x
. To znaczy, że xU i x
. Stąd wynika, że xA lub x B. Jeśli xAch, w takim razie xĀ, co oznacza
. Jeśli xB, to
, co znaczy
. Tym samym każdy element zestawu.
. jest również elementem zestawu
To jest

Udowadniamy teraz odwrotnie, to znaczy, że
. Pozwalać
. Jeśli xĀ, to xU i xA, co oznacza xAB. Stąd wynika, że
. Jeśli
, następnie xU i x B. Znaczy, xAB, to znaczy
. Wynika z tego, że każdy element zestawu
jest również elementem zestawu
, to jest
.

Znaczy,
, co miało zostać udowodnione.

A(BC) = (AB)(AC);

1. Dowód ze schematem:

Pozwalać xA(BC). Następnie x A i x BC. Jeśli xB, to xAB, co nie jest sprzeczne z tym, co zostało powiedziane, co oznacza, że x(AB)(AC). Jeśli xC, to x AC. W związku z tym, x(AB)(AC). Udowodniliśmy więc, że A(BC)  (AB)(AC.

Niech teraz x (AB)(AC). Jeśli xAB, to x A i x B. Stąd wynika, że x A i xС, to znaczy xA(BC). Jeśli xAC, to x A i x C. Stąd wynika, że x A i xС, to znaczy xA(BC). Zatem (AB)(AC) A(BC). Dlatego A(BC) = (AB)(AC). co było do okazania

Dowodząc wystarczalności otrzymaliśmy, że АВ=. Jest oczywiste, że С, więc związek jest udowodniony. W dowodzie uwzględniono przypadek najbardziej ogólny. Jednak nadal istnieje kilka opcji podczas konstruowania diagramów. Na przykład przypadek równości AB \u003d C lub
, przypadek pustych zestawów i tak dalej. Oczywiste jest, że trudno jest wziąć pod uwagę wszystkie możliwe opcje. Dlatego uważa się, że dowód relacji za pomocą diagramów nie zawsze jest poprawny.

2. Dowód za pomocą definicji równości zbiorów.

Potrzebować. Niech ABC i element x A. Pokażmy, że w tym przypadku element zbioru A będzie również elementem zbioru
.

Rozważ dwa przypadki: xW lub
.

Jeśli xB, to xABC, to znaczy xC, a w rezultacie
.

Jeśli
, wtedy i
. Potrzeba została udowodniona.

Niech teraz
oraz xAB. Pokażmy, że element x będzie również elementem zestawu C.

Jeśli xAB, to x A i x B. O ile
, znaczy x C. Udowodniono wystarczalność.

1. Dowód ze schematem:

2. Dowód za pomocą definicji równości zbiorów.

Niech AB. Rozważ element xB (lub
). Podobnie: xA (lub x). Czyli każdy element zestawu jest również elementem zbioru Ā. A może tak być, jeśli
. co było do okazania

Zadanie 3.4. Wyraź symbolicznie wskazane obszary i uprość wynikowe wyrażenia.

Rozwiązanie.

Przeszukiwany obszar składa się z dwóch odizolowanych części. Nazwijmy je górnymi i niższymi. Przedstawiony przez nich zestaw można opisać następująco:

M = ( x x A i xW i xC lub x C i x A i x B).

Z definicji operacji na zbiorach otrzymujemy:

M = ((AB)\C)(C\A\B).

Napiszmy to wyrażenie za pomocą podstawowych operacji - dodawania, sumy i przecięcia:

Nie da się uprościć tego wyrażenia, ponieważ mamy jedno wystąpienie każdego znaku. To najprostsza forma tej formuły.

Obszar ten można uznać za sumę zbiorów A\B\C i ABC. Z definicji M = ( x x A i xW i xC lub x A i xW i x C). Uprośćmy:

Zadania do samodzielnego rozwiązania.

1. Uproszczać:

2. Udowodnij za pomocą diagramów, praw algebry zbiorów i definicji równości zbiorów:

(AB)\B = A\B;

A(BC) = A\(A\B)(A\C);

AB \u003d AB  A \u003d B;

A \ B \u003d   AB \u003d A.

3. Dowiedz się, czy istnieje zbiór X, który spełnia dowolną A równość:

AX \u003d A; (odpowiedź );

W rozdziale 8 uwzględniono takie typy obiektów o charakterze nienumerycznym, jak zbiory rozmyte i losowe. Celem tego dodatku jest głębsze zbadanie własności zbiorów rozmytych i wykazanie, że teoria zbiorów rozmytych w pewnym sensie sprowadza się do teorii zbiorów losowych. Aby osiągnąć ten cel, formułuje się i dowodzi łańcuch twierdzeń.

W dalszej części zakłada się, że wszystkie rozważane zbiory rozmyte są podzbiorami tego samego zbioru Y.

P2-1. Prawa de Morgana dla zbiorów rozmytych

Jak wiadomo, następujące tożsamości algebry zbiorów nazywamy prawami Morgana:

Twierdzenie 1.W przypadku zbiorów rozmytych tożsamości

(3)

Dowód Twierdzenia 1 polega na bezpośredniej weryfikacji poprawności relacji (2) i (3) poprzez obliczenie wartości funkcji przynależności zbiorów rozmytych uczestniczących w tych relacjach na podstawie definicji podanych w rozdziale 8.

Tożsamości (2) i (3) będą nazywane Prawa de Morgana dla zbiorów rozmytych. W przeciwieństwie do klasycznego przypadku relacji (1), składają się one z czterech tożsamości, z których jedna para odnosi się do operacji sumy i przecięcia, a druga do operacji iloczynu i sumy. Podobnie jak relacja (1) w algebrze zbiorów, prawa de Morgana w algebrze zbiorów rozmytych pozwalają przekształcać wyrażenia i formuły zawierające operacje negacji.

P2-2. Prawo rozdzielcze dla zbiorów rozmytych

Niektóre właściwości operacji na zbiorach nie dotyczą zbiorów rozmytych. Tak, z wyjątkiem sytuacji, gdy A- zestaw "wyczyść" (tzn. funkcja przynależności przyjmuje tylko wartości 0 i 1).

Czy prawo dystrybucji jest prawdziwe dla zbiorów rozmytych? W literaturze czasem niejasno stwierdza się, że „nie zawsze”. Wyjaśnijmy to całkowicie.

Twierdzenie 2.Dla dowolnych zbiorów rozmytych A, B i C

Jednocześnie równość

jest prawdziwe wtedy i tylko wtedy, gdy dla wszystkich

Dowód. Naprawiamy dowolny element. Aby skrócić zapis, oznaczamy Aby udowodnić identyczność (4), należy wykazać, że

Rozważ różne porządki trzech liczb a, b, c. Niech najpierw Wtedy lewa strona relacji (6) jest a prawa strona tj. równość (6) jest ważna.

Niech Wtedy w relacji (6) stoi po lewej i po prawej stronie, czyli relacja (6) jest znowu równością.

Jeśli więc w relacji (6) stoi po lewej i po prawej stronie, tj. obie części ponownie pasują.

Trzy inne porządki liczb a, b, c nie ma potrzeby demontowania, gdyż w związku (6) liczby b oraz C wprowadź symetrycznie. Udowodniono tożsamość (4).

Drugie twierdzenie Twierdzenia 2 wynika z faktu, że zgodnie z definicjami operacji na zbiorach rozmytych (patrz rozdział 8)

Te dwa wyrażenia pokrywają się wtedy i tylko wtedy, kiedy to, czego wymagało udowodnienie.

Definicja 1.Nośnikiem zbioru rozmytego A jest zbiór wszystkich punktów , dla którego

Wniosek z twierdzenia 2.Jeśli nośniki zbiorów rozmytych B i C pokrywają się z Y, to równość (5) zachodzi wtedy i tylko wtedy, gdy A jest zbiorem „czystym” (tj. zwykłym, klasycznym, nie rozmytym).

Dowód. Według warunku ze wszystkimi . Następnie z Twierdzenia 2 wynika, że tych. lub , co oznacza, że A- jasny zestaw.

P2-3. Zbiory rozmyte jako rzuty zbiorów losowych

Od samego początku pojawienia się nowoczesnej teorii rozmytej w latach 60. rozpoczęto dyskusję na temat jej związku z teorią prawdopodobieństwa. Faktem jest, że funkcja przynależności zbioru rozmytego przypomina rozkład prawdopodobieństwa. Jedyna różnica polega na tym, że suma prawdopodobieństw po wszystkich możliwych wartościach zmiennej losowej (lub całki, jeśli zbiór możliwych wartości jest niepoliczalny) jest zawsze równa 1, a suma S wartości funkcji przynależności (w przypadku ciągłym – całka funkcji przynależności) mogą być dowolną liczbą nieujemną. Istnieje pokusa normalizacji funkcji przynależności, tj. podziel wszystkie jego wartości przez S(w S 0), aby zredukować go do rozkładu prawdopodobieństwa (lub gęstości prawdopodobieństwa). Jednak specjaliści od rozmycia słusznie sprzeciwiają się takiej „prymitywnej” redukcji, gdyż jest ona przeprowadzana dla każdego rozmycia (zbioru rozmytego) osobno, a definicje zwykłych operacji na zbiorach rozmytych nie mogą się z nią zgodzić. Niech funkcje przynależności zbiorów rozmytych A oraz V. Jak w tym przypadku przekształcane są funkcje członkostwa? Zainstaluj to w zasadzie niemożliwe. Ostatnie stwierdzenie staje się całkiem jasne po rozważeniu kilku przykładów par zbiorów rozmytych z tymi samymi sumami wartości funkcji przynależności, ale różnymi wynikami operacji na nich opartych na teorii mnogości oraz sumami wartości odpowiadających im funkcji przynależności dla tych wyników operacji mnogościowych, na przykład, dla przecięcia zbiorów są również odrębne.

W pracach nad zbiorami rozmytymi dość często stwierdza się, że teoria rozmyta jest samodzielną gałęzią matematyki stosowanej i nie ma nic wspólnego z teorią prawdopodobieństwa (patrz np. przegląd literatury w monografiach). Autorzy, którzy porównywali teorię rozmytą i teorię prawdopodobieństwa, zwykle podkreślali różnicę między tymi obszarami badań teoretycznych i stosowanych. Zwykle porównuje się aksjomatyki i porównuje obszary zastosowań. Należy od razu zauważyć, że argumenty w drugim typie porównań nie mają mocy dowodowej, ponieważ istnieją różne opinie na temat granic stosowalności nawet tak długiej dziedziny naukowej, jak metody probabilistyczno-statystyczne. Przypomnijmy, że wynik rozumowania jednego z najsłynniejszych matematyków francuskich, Henri Lebesgue, dotyczący granic stosowalności arytmetyki jest następujący: „Arytmetyka ma zastosowanie, gdy ma zastosowanie” (patrz jego monografia).

Porównując różne aksjomaty teorii rozmytej i teorii prawdopodobieństwa, łatwo zauważyć, że listy aksjomatów różnią się. Z tego jednak bynajmniej nie wynika, że ​​między wskazanymi teoriami nie da się ustalić związku, np. znanej redukcji geometrii euklidesowej na płaszczyźnie do arytmetyki (a dokładniej do teorii systemu liczbowego - patrz np. monografia). Przypomnijmy, że te dwie aksjomatyki — geometria euklidesowa i arytmetyka — na pierwszy rzut oka bardzo się różnią.

Można zrozumieć dążenie entuzjastów nowego nurtu do podkreślenia fundamentalnej nowości ich aparatu naukowego. Równie ważne jest jednak ustalenie powiązań między nowym podejściem a dotychczas znanymi.

Jak się okazało, teoria zbiorów rozmytych jest ściśle powiązana z teorią zbiorów losowych. W 1974 roku pokazano w pracy, że naturalne jest traktowanie zbiorów rozmytych jako „rzutów” zbiorów losowych. Rozważmy tę metodę sprowadzania teorii zbiorów rozmytych do teorii zbiorów losowych.

Definicja 2.Pozwalać - losowy podzbiór skończonego zbioru Y. Zbiór rozmyty B zdefiniowany na Y nazywa się rzutem A i jest oznaczony przez Proj A, jeśli

(7)

dla wszystkich

Oczywiście każdy losowy zestaw A można powiązać za pomocą wzoru (7) zbiór rozmyty B = Projekt A. Okazuje się, że jest też odwrotnie.

Twierdzenie 3. Dla dowolnego podzbioru rozmytego B skończonego zbioru Y, istnieje losowy podzbiór A zbioru Y taki, że B = Proj A.

Dowód. Wystarczy określić rozkład zbioru losowego A. Pozwalać 1- przewoźnik V(patrz definicja 1 powyżej). Bez utraty ogólności możemy założyć, że na niektóre m i elementy 1 ponumerowane w taki sposób, że

Przedstawiamy zestawy

Dla wszystkich innych podzbiorów x zestawy Na włóżmy P(A=X)=0. Ponieważ żywioł y t w zestawie T(1), T(2),…, T(t) i nie jest zawarte w zestawy Y(t+1),…, Y(m), następnie z powyższych wzorów wynika, że Jeśli więc, oczywiście, Twierdzenie 3 jest udowodnione.

Rozkład zbioru losowego z elementami niezależnymi, jak wynika z rozważań w rozdziale 8, jest całkowicie zdeterminowany jego rzutowaniem. W przypadku skończonego zbioru losowego o ogólnej formie tak nie jest. Aby wyjaśnić to, co zostało powiedziane, potrzebujemy następującego twierdzenia.

Twierdzenie 4. Dla losowego podzbioru A zbioru Y ze skończonego liczba elementów zbiory liczb oraz są wyrażane przez siebie nawzajem.

Dowód. Drugi zestaw jest wyrażony w kategoriach pierwszego w następujący sposób:



Elementy pierwszego zbioru można wyrazić w kategoriach drugiego za pomocą formuły wtrąceń i wykluczeń z logiki formalnej, zgodnie z którą

W tej formule w pierwszej sumie w przebiega przez wszystkie elementy zestawu Y\X, w drugiej sumie zmienne sumowania 1 oraz o 2 nie pokrywają się, a także przebiegają przez ten zestaw i tak dalej. Odniesienie do formuły włączania i wykluczania uzupełnia dowód Twierdzenia 4.

Zgodnie z Twierdzeniem 4, losowy zbiór A można scharakteryzować nie tylko rozkładem, ale także zbiorem liczb W tym zbiorze a nie ma innych relacji typu równości. Zbiór ten zawiera liczby, dlatego ustalenie rzutu zestawu losowego jest równoznaczne z ustaleniem k = karta (Y) parametry od (2k-1) parametry określające rozkład zbioru losowego A ogólnie.

Przydatne będzie poniższe twierdzenie.

Twierdzenie 5. Jeśli Rzut A = B, następnie

Aby to udowodnić, wystarczy posłużyć się identycznością z teorii zbiorów losowych, wzorem na prawdopodobieństwo przekrycia z rozdziału 8, definicją negacji zbioru rozmytego oraz faktem, że suma wszystkich P(A= X) jest równe 1.

P2-4. Przecięcia i iloczyny zbiorów rozmytych i losowych

Przekonajmy się, jak operacje na zbiorach losowych są powiązane z operacjami na ich rzutach. Na mocy praw de Morgana (Twierdzenie 1) i Twierdzenie 5, wystarczy rozważyć działanie przecięcia zbiorów losowych.

Twierdzenie 6. Jeśli losowe podzbiory A 1 i A 2 zbioru skończonego są niezależne, to zbiór rozmyty jest produktem zbiory rozmyte Proj A 1 i Proj A 2 .

Dowód. Musimy to pokazać za wszelką cenę

Zgodnie ze wzorem na prawdopodobieństwo pokrycia punktu przez zbiór losowy (rozdział 8)

Jak wiadomo, rozkład przecięcia zbiorów losowych można wyrazić w postaci ich łącznego rozkładu w następujący sposób:

Z zależności (9) i (10) wynika, że ​​prawdopodobieństwo pokrycia przecięcia zbiorów losowych można przedstawić jako sumę podwójną

Zauważ teraz, że prawą stronę formuły (11) można przepisać w następujący sposób:

(12)

Rzeczywiście, formuła (11) różni się od formuły (12) tylko tym, że zawiera wyrażenia, w których przecięcie zmiennych sumowania przyjmuje stałą wartość. Korzystając z definicji niezależności zbiorów losowych i zasady mnożenia sum otrzymujemy, że z (11) i (12) wynika równość

Aby uzupełnić dowód Twierdzenia 6, wystarczy jeszcze raz odwołać się do wzoru na prawdopodobieństwo objęcia punktu przez zbiór losowy (rozdział 8).

Definicja 3. Nośnikiem zbioru losowego C jest zbiór wszystkich tych elementów dla którego

Twierdzenie 7.Równość

jest prawdziwe wtedy i tylko wtedy, gdy przecięcie podpór zbiorów losowych oraz pusty.

Dowód. Konieczne jest ustalenie warunków, w jakich

Wtedy równość (13) sprowadza się do warunku

Jest oczywiste, że relacja (14) jest spełniona wtedy i tylko wtedy, gdy R 2 R 3=0 dla wszystkich tj. nie ma takiego elementu, że w tym samym czasie oraz , a to jest równoznaczne z pustką przecięcia podpór zbiorów losowych i . Twierdzenie 7 jest udowodnione.

P2-5. Redukcja ciągu operacji na zbiorach rozmytych

do sekwencji operacji na zbiorach losowych

Powyżej uzyskano pewne powiązania między zbiorami rozmytymi i losowymi. Warto zauważyć, że badanie tych zależności w pracy (praca ta została ukończona w 1974 r. i przedstawiona na seminarium „Wielowariantowa analiza statystyczna i modelowanie probabilistyczne procesów rzeczywistych” w dniu 18 grudnia 1974 r. – patrz) rozpoczęło się wprowadzeniem losowych zbiory w celu opracowania i uogólnienia aparatury zbiorów rozmytych L. Zadeh. Faktem jest, że aparat matematyczny zbiorów rozmytych nie pozwala na właściwe uwzględnienie różnych opcji relacji między modelowanymi za jego pomocą pojęciami (obiektami) i nie jest wystarczająco elastyczny. Tak więc, aby opisać "część wspólną" dwóch zbiorów rozmytych, są tylko dwie operacje - iloczyn i przecięcie. Jeśli pierwszy z nich zostanie użyty, to faktycznie zakłada się, że zbiory zachowują się jak rzuty niezależnych zbiorów losowych (patrz Twierdzenie 6 powyżej). Operacja przecięcia również nakłada dobrze zdefiniowane ograniczenia na rodzaj zależności między zbiorami (patrz Twierdzenie 7 powyżej), a w tym przypadku nawet występują warunki konieczne i wystarczające. Pożądane jest posiadanie większych możliwości modelowania zależności między zbiorami (pojęciami, obiektami). Takie możliwości daje zastosowanie aparatu matematycznego zbiorów losowych.

Celem redukcji zbiorów rozmytych do losowych jest zobaczenie za każdą konstrukcją ze zbiorów rozmytych konstrukcji ze zbiorów losowych, która określa właściwości pierwszego z nich, tak jak widzimy zmienną losową przez gęstość rozkładu prawdopodobieństwa. W tym podrozdziale przedstawiamy wyniki redukcji algebry zbiorów rozmytych do algebry zbiorów losowych.

Definicja 4.Przestrzeń prawdopodobieństwa { W, G, P)podzielmy, jeśli dla dowolnego zbioru mierzalnego X G i dowolnej liczby dodatniej, mniejsze niż P(X), można określić zbiór mierzalny taki, że

Przykład. Niech będzie jednostkowym sześcianem skończenie wymiarowej przestrzeni liniowej, g jest sigma-algebrą zbiorów borelowskich, i P jest miarą Lebesgue'a. Następnie { W, G, P)- podzielna przestrzeń prawdopodobieństwa.

Podzielna przestrzeń prawdopodobieństwa nie jest więc egzotyczna. Przykładem takiej przestrzeni jest zwykły sześcian.

Dowód twierdzenia sformułowanego w przykładzie przeprowadza się za pomocą standardowych sztuczek matematycznych polegających na tym, że zbiór mierzalny można arbitralnie aproksymować za pomocą zbiorów otwartych, przy czym te ostatnie są reprezentowane jako suma co najwyżej policzalnej liczby kul otwartych, a podzielność dla kul jest sprawdzana bezpośrednio (od kuli X korpus o objętości oddzielony odpowiednią płaszczyzną).

Twierdzenie 8.Niech zbiór losowy A będzie podany na podzielnej przestrzeni prawdopodobieństwa (W, G, P) o wartościach w zbiorze wszystkich podzbiorów zbioru Y o skończonej liczbie elementów oraz zbioru rozmytego D na Y. Wtedy są zbiory losowe ~1, Od 2, Od 3, C 4 na tej samej przestrzeni prawdopodobieństwa takiej, że

gdzie B = ProjA.

Dowód. Ze względu na ważność praw de Morgana dla rozmytych (patrz Twierdzenie 1 powyżej) i dla zbiorów losowych, a także Twierdzenie 5 powyżej (o negacjach), wystarczy udowodnić istnienie zbiorów losowych Od 1 oraz Od 2 .

Rozważ rozkład prawdopodobieństwa w zbiorze wszystkich podzbiorów zbioru Na, odpowiadający losowemu zestawowi Z takie, że Rzut C = D(istnieje na mocy Twierdzenia 3). Zbudujmy losowy zestaw C 2 Wyklucz element tylko dla z tego samego zbioru Y takie, że

a ponadto wyniki operacji mnogościowych są powiązane podobnymi relacjami

gdzie znak oznacza, że ​​rozpatrywane miejsce jest symbolem przecięcia zbiorów losowych, jeżeli definicja B m zawiera symbol przecięcia lub symbol iloczynu zbiorów rozmytych i odpowiednio symbol sumy zbiorów losowych, jeśli B m zawiera symbol unii lub symbol sumy zbiorów rozmytych.