Теперь подробнее обсудим величину DU (которая представляет в расчетах изменение внутренней энергии) применительно к проводнику, по которому начинает течь ток.
Постепенно, выбранный проводник будет нагреваться, а это значит, что будет увеличиваться его внутренняя энергия. По мере нагрева разность между температурой проводника и окружающей его среды будет увеличиваться. Согласно закономерности Ньютона, вместе с этим возрастать будет и мощность теплоотдачи проводника. Таким образом, через какое-то время температура проводника, достигнув определенного значения, перестанет увеличиваться. В этот момент величина DU будет равной нулю, и перестанет изменяться внутренняя энергия проводника.
Тогда для этого состояния первый закон термодинамики будет выглядеть так: A = – Q . То есть когда не меняется внутренняя энергия проводника, работа тока целиком превращается в теплоту. Используя этот вывод, можем записать все три рассмотренные формулы для расчета работы тока в несколько ином виде, в конечном итоге получаем закон Джоуля-Ленца в интегральной форме:
Закон Джоуля-Ленца в дифференциальной форме выглядит совершенно по-иному, мы рассмотрим только общий вариант, без дополнительных выведений и вычислений, который выглядит так:
![]() Где:
Где:
Так в общих чертах выглядит закон Джоуля-Ленца и его интегральная и дифференциальная формы. Хотя, если проводить дальнейшие вычисления, то закон может принимать и другие формы.
21. Закон Ома для неоднородного участка цепи (обобщенный закон Ома). Закон Ома для замкнутой цепи.
Участок цепи, содержащий источник ЭДС, называется неоднородным (рис.5.11). Всякий источник ЭДС характеризуется величиной ЭДС ε ивнутренним сопротивлением r .
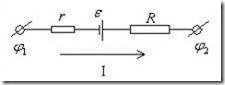
Напряжение на концах участка цепи.
Рис.5.11 . Неоднородный участок цепи.
Закон Ома для неоднородного участка цепи имеет вид:
![]()
При соединении концов неоднородного участка цепи идеальным проводником образуется замкнутая цепь, в которойпотенциалы φ 1 иφ 2 выравниваются и мы приходим к закону Ома для замкнутой (или полной ) цепи :
Если сопротивление внешней цепи , то имеем случай короткого замыкания . В этом случае в цепи течетмаксимальный ток:
При имеем разомкнутую цепь . В этом случае ток в цепи равен нулю :
22. Правила Кирхгофа для разветвленных цепей постоянного тока
Правило 1 : в любом узле сумма входящих токов и выходящих равна нулю. Оно учитывает закон сохранения электрического заряда.
При этом токи, идущие к узлу, и токи, исходящие из узла, следует считать величинами разных знаков.
Правило 2 : алгебраическая сумма произведений сил токов на сопротивления при обходе контура равна сумме ЭДС в контуре. Учитывается закон сохранения энергии.
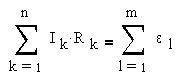
Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа , которые являются обобщением закона Ома на случай разветвленных цепей.
В разветвленных цепях можно выделить узловые точки (узлы ), в которых сходятся не менее трех проводников (рис. 1.10.1). Токи, втекающие в узел, принято считать положительными; вытекающие из узла – отрицательными.
В узлах цепи постоянного тока не может происходить накопление зарядов. Отсюда следует первое правило Кирхгофа :
Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:
|
Первое правило Кирхгофа является следствием закона сохранения электрического заряда .
В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называются контурами . На разных участках выделенного контура могут протекать различные токи. На рис. 1.10.2 представлен простой пример разветвленной цепи. Цепь содержит два узла a и d , в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d ).
В цепи можно выделить три контура abcd , adef и abcdef . Из них только два являются независимыми (например, abcd и adef ), так как третий не содержит никаких новых участков.
Второе правило Кирхгофа является следствием обобщенного закона Ома .
Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 1.10.2, например, abcd . Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура . При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис. 1.10.3.
Для участков контура abcd обобщенный закон Ома записывается в виде:
Для участка bc : I 1 R 1 = Δφ bc – 1 .
Для участка da : I 2 R 2 = Δφ da – 2 .
Складывая левые и правые части этих равенств и принимая во внимание, что Δφ bc = – Δφ da , получим:
Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура .
Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов в электрической цепи. Для цепи, изображенной на рис. 1.10.2, система уравнений для определения трех неизвестных токов I 1 , I 2 и I 3 имеет вид:
|
I 1 R 1 + I 2 R 2 = – 1 – 2 , |
|
– I 2 R 2 + I 3 R 3 = 2 + 3 , |
|
– I 1 + I 2 + I 3 = 0 |
23. Работа и мощность постоянного электрического тока. КПД источника тока.
Работа А электрического тока на участке цепи с электрическим сопротивлением R за время D t равна:
A = I · U · ? t = I 2 · R · ? t
Мощность P электрического тока равна отношению работы А тока ко времени D t, за которое эта работа совершена:
P = A / ? t = I · U = I 2 R = U 2 / R.
Работа А электрического тока равна количеству теплоты Q, выделяемому проводником (если не совершается механическая работа и не происходят химические реакции):
Q = I 2 · R · ? t
Этот закон был экспериментально установлен английским ученым Джеймсом Джоулем (1818-1889) и русским ученым Эмилием Ленцем (1804-1865) и поэтому носит название закона Джоуля - Ленца .
Рассмотрим элементарную электрическую цепь, содержащую источник ЭДС с внутренним сопротивлением r , и внешним сопротивлением R (рис. 7.5).
КПД всегда определяем как отношение полезной работы к затраченной:
|
|
Полезная работа – мощность, выделяемая на внешнем сопротивлении R в единицу времени. По закону Ома имеем: а тогда
![]() .
.
24. Вывод закона Ома из классической теории электропроводимости металлов.
Друде считал, что сразу после очередного соударения электрона с ионом кристаллической решетки скорость упорядоченного движения электрона равна нулю. Предположим, что напряженность поля не изменяется. Тогда под действием поля электрон получит постоянное ускорение равное
и к концу пробега скорость упорядоченного движения достигнет значения
|
|
где t - среднее время между двумя последовательными соударениями электрона с ионами решетки. Друде не учитывал распределение электронов по скоростям и приписывал всем электронам одинаковое значение средней скорости . В этом приближении , где - среднее значение длины свободного пробега, - скорость теплового движения электронов. Подставим это значение t в формулу (18.2)
Скорость изменяется за время пробега линейно. Поэтому ее среднее (за пробег) значение равно половине максимального
![]()
Подставив это выражение в
Плотность тока оказалась пропорциональной напряженности поля. Следовательно, мы получили закон Ома. Согласно коэффициент пропорциональности между j и Е представляет собой проводимость
Если бы электроны не сталкивались с ионами решетки, длина свободного пробега, а, следовательно, и проводимость были бы бесконечно велики. Таким образом, электрическое сопротивление металлов обусловлено соударениями свободных электронов с ионами.
Вывод закона Джоуля-Ленца из классической теории электропроводности металлов. Затруднения этой теории.
К концу свободного пробега электрон приобретает скорость , и, следовательно, дополнительную кинетическую энергию, средняя величина которой
![]()
Столкнувшись с ионом, электрон по предположению полностью теряет приобретенную им за время пробега скорость, и передает энергию кристаллической решетке. Эта энергия идет на увеличение внутренней энергии металла, проявляющееся в его нагревании. Каждый электрон претерпевает за секунду в среднем 1/t соударений, сообщая всякий раз решетке энергию . Следовательно, в единице объема за единицу времени должно выделяться тепло
![]()
где n - число электронов проводимости в единице объема. Величина есть не что иное, как удельная мощность тока. Множитель при совпадает со значением (18.3) для закона Ома. Таким образом. Мы пришли к выражению закона Джоуля-Ленца в дифференциальной форме.
Теплоемкость металлов. Теплоемкость металла складывается из теплоемкости его кристаллической решетки и теплоемкости электронного газа. Поэтому атомная (т. е. рассчитанная на 1 моль) теплоемкость металла должна быть значительно большей, чем атомная теплоемкость диэлектриков, у которых нет свободных электронов. Согласно закону Дюлонга и Пти (см. §73), теплоемкость одноатомного кристалла равна 3R . Учтем, что теплоемкость одноатомного электронного газа равна 3 / 2 R . Тогда атомная теплоемкость металлов должна быть близка к 4,5R . Однако опыт доказывает, что она равна 3R, т. е. для металлов, так же как и для диэлектриков, хорошо выполняется закон Дюлонга и Пти. Следовательно, наличие электронов проводимости практически не сказывается на значении теплоемкости, что не объясняется классической электронной теорией.
Указанные расхождения теории с опытом можно объяснить тем, что движение электронов в металлах подчиняется не законам классической механики, а законам квантовой механики и, следовательно, поведение электронов проводимости надо описывать не статистикой Максвелла - Больцмана, а квантовой статистикой. Поэтому объяснить затруднения элементарной классической теории электропроводности металлов можно лишь квантовой теорией, которая будет рассмотрена в дальнейшем. Надо, однако, отметить, что классическая электронная теория не утратила своего значения и до настоящего времени, так как во многих случаях (например, при малой концентрации электронов проводимости и высокой температуре) она дает правильные качественные результаты и является по сравнению с квантовой теорией простой и наглядной.
Несамостоятельный и самостоятельный газовые разряды.
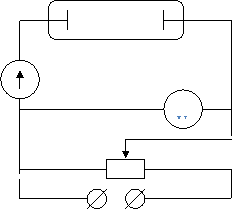
Несамостоятельный газовый разряд. Процесс прохождения электрического тока через газ называется газовым разрядом. Если электропроводность газа создается внешними ионизаторами, то электрический ток, возникающий в нем, называется несамостоятельным газовым разрядом. С прекращением действия внешних ионизаторов несамостоятельный разряд прекращается. Несамостоятельный газовый разряд не сопровождается свечением газа. Ниже изображен график зависимости силы тока от напряжения при несамостоятельном разряде в газе. Для построения графика использовалась стеклянная трубка с двумя впаянными в стекло металлическими электродами. Цепь собрана как показано на рисунке ниже.
|
|
Самостоятельный
газовый разряд.
Электрический разряд в газе, сохраняющийся после прекращения действия внешнего ионизатора, называется самостоятельным газовым разрядом . Для его осуществления необходимо, чтобы в результате самого разряда в газе непрерывно образовывались свободные заряды. Основным источником их возникновения является ударная ионизация молекул газа.
Если после достижения насыщения продолжать увеличивать разность потенциалов между электродами, то сила тока при достаточно большом напряжении станет резко возрастать (график 2).
Это означает, что в газе появляются дополнительные ионы, которые образуются за счет действия ионизатора. Сила тока может возрасти в сотни и тысячи раз, а число заряженных частиц, возникающих в процессе разряда, может стать таким большим, что внешний ионизатор будет уже не нужен для поддержания разряда. Поэтому ионизатор теперь можно убрать.
|
|
27. Магнитное поле, Магнитная индукция. Принцип суперпозиции магнитных полей. Закон Ампера.
Зако́н Ампе́ра - закон взаимодействия электрических токов . Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных - отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила , с которой магнитное поле действует на элемент объёма проводника с током плотности , находящегося в магнитном поле с индукцией :
![]() .
.
Модуль силы Ампера можно найти по формуле:
где - угол между векторами магнитной индукции и тока.
Сила максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции ():
Магни́тное по́ле - силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом , независимо от состояния их движения , магнитная составляющая электромагнитного поля
Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты ).
Магни́тная инду́кция - векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .
Более конкретно, - это такой вектор, что сила Лоренца , действующая со стороны магнитного поля на заряд , движущийся со скоростью , равна
![]()
где косым крестом обозначено векторное произведение , α - угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика ).
И диффеpенциальной фоpмах
Пpи пpохождении электрического тока чеpез пpоводник, обладающий сопpотивлением R выделяется теплота. Если проводник неподвижен и в нем не совершаются химические реакции, то количество теплоты, выделяющееся на одноpодном участке цепи опpеделяется по фоpмуле
dQ = I Udt = I 2 R = U 2 / R, (2.24)
где dt - вpемя пpохождения тока.
Эта фоpмула выpажает закон Джоуля-Ленца в интегpальной фоpме .
Выведем более общую фоpму закона Джоуля-Ленца, спpаведливую для любой точки пpоводника, одноpодного или неодноpодного, с пеpеменным сечением. Для этого пpедставим себе элементаpный объем пpоводника dV в виде цилиндрика (обpазующая его паpаллельна вектоpу j ) с попеpечным сечением ds и длиной dl . Количество теплоты, выделяющееся в том объеме при протекании по нему тока
dQ = I 2 Rdt = I 2 (rdl /ds) dt = rj 2 dVdt. (2.25)
Здесь dV = ds . dl - объём цилиндpика.
Количество теплоты, выделяющееся в единицу объёма пpо-водящей сpеды за еденицу вpемени, называется удельной тепловой мощностью тока
Q уд = dQ/dVdt. (2.26)
Из выражений (2.26) и (2.25) с учетом (2.16) следует
Q уд = rj 2 = (1/g) (gE) 2 = gE 2 .
Q уд = gE 2 (2.27)
является обобщенным выражением закона Джоуля- Ленца в дифференциальной форме, пригодном для любого проводника.
Правила Кирхгофа
В основе расчета сложных электрических цепей постоянного тока лежат правила Кирхгофа.
Первое правило , которому подчиняются стационарные токи, можно записать в виде n
S I i = 0. (2.28)
В каждом узле разветвленной цепи сумма входящих токов равна сумме выходящих, т.е. алгебраическая сумма токов, сходящихся в узле, равна нулю. Это правило выражает закон сохранения заряда. В противном случае в узлах накапливались бы электрические заряды.
I 3 Узел I 1
Узлом разветвленной цепи назовем точку, в которой сходятся не менее трех проводников (рис. 2.3,а). Токи, направленные к узлу, будем называть входящими. Токи противоположной направленности - выходящими. Для узла, изображенного на рис. 2.3,б первое правило выразится соотношением
I 1 + I 3 - I 2 - I 4 = 0 . (2.29)
Контур - любая замкнутая часть цепи. Например, на рис.2.4 участок e 1 Вe 2 СR 2 R 1 e 1 представляет собой контур. Второе правило Кирхгофа является обобщением закона Ома и относится к любому контуру разветвленной электрической цепи.
Алгебраическая сумма произведений сил токов на сопротивления, включая и внутренние, вдоль замкнутого контура равна сумме электродвижущих сил, включенных в этот контур:
S I i R i + S I i r i = S e i . (2.30)
i = 1 i = 1 i = 1
I 1 e 1 - + e 3 + -
При составлении уравнений по второму правилу Кирхгофа руководствуйтесь следующими правилами.
1. Выберите направление обхода контура либо по часовой, либо против часовой стрелки.
2. Произвольно выберите и обозначьте на схеме электрической цепи направление токов.
3. Если направление обхода контура совпадает с направлением тока, произведение I i R i берем со знаком " + ". В противном случае - со знаком " - ".
4. Если при обходе контура внутри источника ток идет от отрицательного полюса к положительному, перед e i ставится знак "+", а если наоборот - знак " -".
Имейте ввиду, что уравнения по первому и второму правилу Кирхгофа составляют не длявсех узлов схемы и не длявсех контуров, и что число неизвестных токов не всегда равно числу сопротивлений. Для правильного обозначения сил токов в цепи подсчитайте число ветвей р . Ветвью называется любой участок цепи, соединяющий два соседних узла. Число токов должно быть равно числу ветвей. В каждой ветви течет только один ток, независимо от числа сопротивлений в ней, например, в схеме на рис. 2.4 в ветви Be 1 R 1 R 2 С два сопротивления R 1 и R 2 , но ток в ней течет один, I 1 .
Обозначим число узлов в схеме m. Число уравнений по первому правилу Кирхгофа должно быть на единицу меньше, т. е. (m - 1), а по второму разность - между числом ветвей p и числом уравнений по первому правилу - (p - m + 1). В общей сложности число уравнений, составленных по тому и другому правилу, должно быть равным p , т. е. числу неизвестных токов.
При составлении уравнений по второму правилу Кирхгофа нужно всякий раз выбирать контуры с новыми неизвестными токами. Тогда составляемые уравнения будут линейно независимы, а система уравнений - решаемой.
Для схемы на рис. 2.4 число узлов m = 2, число ветвей p = 3.
По первому правилу Кирхгофа надо составить одно уравнение, а по второму - два. Система уравнений для определения токов имеет вид:
Для точки В: I 1 - I 2 + I 3 = 0, (2.31)
Для контура e 1 Вe 2 С R 1 R 2 e 1:
I 1 (R 1 + R 2 + r 1) + I 2 r 2 = e 1 + e 2 , (2.32)
Для контура Вe 3 R 3 Сe 2 В
I 2 r 2 - I 2 (r 3 + R 3) = -e 2 -e 3 . (2.33)
При известных сопротивлениях R 1 , R 2 , R 3 , r 1 , r 2 , r 3 совместное решение уравнения (2.31) - (2.33) позволяет определить токи, текущие во всех ветвях цепи.
Ниже приведены некоторые типовые экзаменационные задания.
ПОСТОЯННЫЙ ТОК
Какое количество электричества q было перенесено через поперечное сечение проводника, если ток равномерно возрастал от нуля до 3 А в течение 20 с?7. Сила тока в проводнике меняется по закону, приведенному на графике. Определить заряд, прошедший через поперечное сечение проводника за 1 мин. Сопротивление проводника 10 Ом.
8. ЭДС батареи равна 1,60 В. При замыкании ее на нагрузку сопротивлением 3 Ом напряжение на полюсах батареи становится равным 0,96 В. Найти внутреннее сопротивление батареи.
9. При разомкнутом ключе напряжение на зажимах источника тока равно 6 В, при замкнутом ключе - 4 В. Найти сопротивление цепи, если внутреннее сопротивление источника 1 Ом.
11.
1) 30 Ом 2) 200 Ом 3) 0,15 Ом 4) 6,6 Ом
12. Сопротивление участка цепи, изображенное на рисунке, равно
| R 1 = 10 Ом R 2 = 20 Ом R 2 = 20 Ом |
| R 1 = 10 Ом R 2 = 3 Ом R 3 = 6 Ом |
1) 19 Ом 2) 12 Ом 3) 36 Ом 4) 6,6 Ом
14. 40. Определить полное сопротивление цепи для случаев, изображенных на рис. (а –е). R 1 = 10 Ом, R 2 = 20 Ом, R 3 = 30 Ом. Сопротивлениями проводов пренебречь.
15. По медному проводнику диаметром 1 мм течет ток силой 1 А. Определить напряженность поля внутри проводника.
16. Найти падение напряжения U и плотность тока j на медном проводе длиной l = 500 м и диаметром d = 2 мм, если ток в нем I = 2 А.
17. В результате изменения напряжения мощность электрического тока возросла втрое. Как изменился при этом импульс направленного движения свободных электронов?
| R, Ом Т 0 T , К |
19. Какое явление отражено на приведенном графике зависимости сопротивления проводника R от абсолютной температуры T ?
20. Сопротивление подводящих проводов равно R 1 . Их заменили на провода вдвое большего диаметра из того же материла. Во сколько раз увеличился ток?
21. По алюминиевому отрезку провода длиной 1 м и диаметром 2 мм течет постоянный ток силой 1 А. Определить падение напряжение на нем.
22. . Определить число электронов, проходящих в 1 с через единицу площади поперечного сечения железной проволоки длиной 10 м при напряжении на её концах 6 В.
23. Два сопротивления R 1 = 3 Ом и R 2 = 5 Ом соединены параллельно и подключены к источнику тока с ε = 10 В и r = 1 Ом. Нарисовать электрическую схему такого соединения. Найти ЭДС источника, если сила тока через первое сопротивление 0,65 А..
К сети напряжением 220 В подключена нагрузка 30 Ом. Определить ток, протекающий по нагрузке, если длина подводящих алюминиевых проводов составляет 1 м при толщине 2 мм.28. Вычислить количество тепла, выделяющееся за 2 с на сопротивлении 10 Ом, если по нему течет ток, изменяющийся по закону I = (1 + 2t 2), A.
29. Определить площадь сечения нихромовой проволоки длиной 50 м, необходимой для наматывания реостата, рассчитанного на максимальный ток 1 А и максимальную мощность 100 Вт?
30. По сети длиной 5 км необходимо передать энергию от источника с напряжением 110 В и имеющего мощность 5 кВт. Какого минимального диаметра должен быть медный провод, чтобы потери энергии в сети не превышали 10% от мощности источника?
31. Сколько витков нихромовой проволоки диаметром d = 1 мм нужно навить на фарфоровый цилиндр радиусом r = 2,5 см, чтобы получить печь сопротивлением R = 100 Ом?
32. Два сопротивления 10 и 20 Ом соединены последовательно и включены в электрическую сеть. Какое из них нагревается сильнее и почему?
33. ЭДС источника тока равна 7 В. КПД источника 40 %. Мощность, выделяемая на внешнем сопротивлении равна 4 Вт. Найти это сопротивление.
34. Электрическая цепь состоит из двух последовательно соединенных источников постоянного тока 9 В и 12 В, имеющих внутренние сопротивления 2 Ом и 5 Ом соответственно. Чему равна сила тока в цепи, если внешнее сопротивление цепи равно 50 Ом? Каков КПД элементов?
35. На электроплитку мощностью 600 Вт поставили чайник, вмещающий 1,5 л воды. Через какое время чайник закипит? Температура окружающей среды 20°С, КПД плитки 80 %, удельная теплоемкость воды 4190 Дж/кг·К.
36. Для того, чтобы вскипятить воду на электроплитке, требуется количество теплоты, равное 66 КДж. Сколько для этого понадобится времени при мощности плитки 110 Вт?
37. Уходя на занятия, вы забыли выключить электроплиту мощностью 800 Вт, за что пришлось заплатить по счетчику 5 руб при тарифе 46 коп за кВт·час. Полагая потери электроэнергии в проводах равными 10% от затраченной, определить, сколько времени работала плита.
38. Чтобы быстрее вскипятить воду в стакане, обмотки двух одинаковых нагревателей нужно соединить
1) последовательно 2) параллельно 3) не имеет значения как
4) нельзя ответить без дополнительных условий
39. Имеется 120-вольтовая электрическая лампочка мощностью 60 Вт. Какое добавочное сопротивление R нужно подключить последовательно с лампочкой, чтобы она давала нормальный накал при напряжении в сети U 0 = 220 В?
40. Два стержня, алюминиевый и медный) одинакового размера и формы последовательно подсоединены к источнику тока. На котором из них выделяется больше энергии и во сколько раз?
Какой длины l потребуется нихромовый проводник диаметром 0,5 мм, чтобы изготовить электрический камин, работающий от сети 220 В и дающий 1 МДж в час?43. Точка А - узел электрической схемы. I 1 ,= 5 А, I 2 =2 А, I 3 = 3 А. Определить ток I 4 .
Теперь подробнее обсудим величину DU (которая представляет в расчетах изменение внутренней энергии) применительно к проводнику, по которому начинает течь ток.
Постепенно, выбранный проводник будет нагреваться, а это значит, что будет увеличиваться его внутренняя энергия. По мере нагрева разность между температурой проводника и окружающей его среды будет увеличиваться. Согласно закономерности Ньютона, вместе с этим возрастать будет и мощность теплоотдачи проводника. Таким образом, через какое-то время температура проводника, достигнув определенного значения, перестанет увеличиваться. В этот момент величина DU будет равной нулю, и перестанет изменяться внутренняя энергия проводника.
Тогда для этого состояния первый закон термодинамики будет выглядеть так: A = – Q . То есть когда не меняется внутренняя энергия проводника, работа тока целиком превращается в теплоту. Используя этот вывод, можем записать все три рассмотренные формулы для расчета работы тока в несколько ином виде, в конечном итоге получаем закон Джоуля-Ленца в интегральной форме:
Закон Джоуля-Ленца в дифференциальной форме выглядит совершенно по-иному, мы рассмотрим только общий вариант, без дополнительных выведений и вычислений, который выглядит так:
![]() Где:
Где:
Так в общих чертах выглядит закон Джоуля-Ленца и его интегральная и дифференциальная формы. Хотя, если проводить дальнейшие вычисления, то закон может принимать и другие формы.
21. Закон Ома для неоднородного участка цепи (обобщенный закон Ома). Закон Ома для замкнутой цепи.
Участок цепи, содержащий источник ЭДС, называется неоднородным (рис.5.11). Всякий источник ЭДС характеризуется величиной ЭДС ε ивнутренним сопротивлением r .

Напряжение на концах участка цепи.
Рис.5.11 . Неоднородный участок цепи.
Закон Ома для неоднородного участка цепи имеет вид:
![]()
При соединении концов неоднородного участка цепи идеальным проводником образуется замкнутая цепь, в которойпотенциалы φ 1 иφ 2 выравниваются и мы приходим к закону Ома для замкнутой (или полной ) цепи :
Если сопротивление внешней цепи , то имеем случай короткого замыкания . В этом случае в цепи течетмаксимальный ток:
При имеем разомкнутую цепь . В этом случае ток в цепи равен нулю :
22. Правила Кирхгофа для разветвленных цепей постоянного тока
Правило 1 : в любом узле сумма входящих токов и выходящих равна нулю. Оно учитывает закон сохранения электрического заряда.
При этом токи, идущие к узлу, и токи, исходящие из узла, следует считать величинами разных знаков.
Правило 2 : алгебраическая сумма произведений сил токов на сопротивления при обходе контура равна сумме ЭДС в контуре. Учитывается закон сохранения энергии.
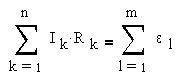
Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа , которые являются обобщением закона Ома на случай разветвленных цепей.
В разветвленных цепях можно выделить узловые точки (узлы ), в которых сходятся не менее трех проводников (рис. 1.10.1). Токи, втекающие в узел, принято считать положительными; вытекающие из узла – отрицательными.
В узлах цепи постоянного тока не может происходить накопление зарядов. Отсюда следует первое правило Кирхгофа :
Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:
|
Первое правило Кирхгофа является следствием закона сохранения электрического заряда .
В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называются контурами . На разных участках выделенного контура могут протекать различные токи. На рис. 1.10.2 представлен простой пример разветвленной цепи. Цепь содержит два узла a и d , в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d ).
В цепи можно выделить три контура abcd , adef и abcdef . Из них только два являются независимыми (например, abcd и adef ), так как третий не содержит никаких новых участков.
Второе правило Кирхгофа является следствием обобщенного закона Ома .
Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 1.10.2, например, abcd . Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура . При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис. 1.10.3.
Для участков контура abcd обобщенный закон Ома записывается в виде:
Для участка bc : I 1 R 1 = Δφ bc – 1 .
Для участка da : I 2 R 2 = Δφ da – 2 .
Складывая левые и правые части этих равенств и принимая во внимание, что Δφ bc = – Δφ da , получим:
|
I 1 R 1 + I 2 R 2 = Δφ bc + Δφ da – 1 + 2 = – 1 – 2 . |
Аналогично, для контура adef можно записать:
|
– I 2 R 2 + I 3 R 3 = 2 + 3 . |
Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура .
Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов в электрической цепи. Для цепи, изображенной на рис. 1.10.2, система уравнений для определения трех неизвестных токов I 1 , I 2 и I 3 имеет вид:
|
I 1 R 1 + I 2 R 2 = – 1 – 2 , |
|
– I 2 R 2 + I 3 R 3 = 2 + 3 , |
|
– I 1 + I 2 + I 3 = 0 |
23. Работа и мощность постоянного электрического тока. КПД источника тока.
Работа А электрического тока на участке цепи с электрическим сопротивлением R за время D t равна:
A = I · U · ? t = I 2 · R · ? t
Мощность P электрического тока равна отношению работы А тока ко времени D t, за которое эта работа совершена:
P = A / ? t = I · U = I 2 R = U 2 / R.
Работа А электрического тока равна количеству теплоты Q, выделяемому проводником (если не совершается механическая работа и не происходят химические реакции):
Q = I 2 · R · ? t
Этот закон был экспериментально установлен английским ученым Джеймсом Джоулем (1818-1889) и русским ученым Эмилием Ленцем (1804-1865) и поэтому носит название закона Джоуля - Ленца .
Рассмотрим элементарную электрическую цепь, содержащую источник ЭДС с внутренним сопротивлением r , и внешним сопротивлением R (рис. 7.5).
КПД всегда определяем как отношение полезной работы к затраченной:
|
|
Полезная работа – мощность, выделяемая на внешнем сопротивлении R в единицу времени. По закону Ома имеем: а тогда
![]() .
.
24. Вывод закона Ома из классической теории электропроводимости металлов.
Друде считал, что сразу после очередного соударения электрона с ионом кристаллической решетки скорость упорядоченного движения электрона равна нулю. Предположим, что напряженность поля не изменяется. Тогда под действием поля электрон получит постоянное ускорение равное
и к концу пробега скорость упорядоченного движения достигнет значения
|
|
где t - среднее время между двумя последовательными соударениями электрона с ионами решетки. Друде не учитывал распределение электронов по скоростям и приписывал всем электронам одинаковое значение средней скорости . В этом приближении , где - среднее значение длины свободного пробега, - скорость теплового движения электронов. Подставим это значение t в формулу (18.2)
Скорость изменяется за время пробега линейно. Поэтому ее среднее (за пробег) значение равно половине максимального
![]()
Подставив это выражение в
Плотность тока оказалась пропорциональной напряженности поля. Следовательно, мы получили закон Ома. Согласно коэффициент пропорциональности между j и Е представляет собой проводимость
Если бы электроны не сталкивались с ионами решетки, длина свободного пробега, а, следовательно, и проводимость были бы бесконечно велики. Таким образом, электрическое сопротивление металлов обусловлено соударениями свободных электронов с ионами.
Вывод закона Джоуля-Ленца из классической теории электропроводности металлов. Затруднения этой теории.
К концу свободного пробега электрон приобретает скорость , и, следовательно, дополнительную кинетическую энергию, средняя величина которой
![]()
Столкнувшись с ионом, электрон по предположению полностью теряет приобретенную им за время пробега скорость, и передает энергию кристаллической решетке. Эта энергия идет на увеличение внутренней энергии металла, проявляющееся в его нагревании. Каждый электрон претерпевает за секунду в среднем 1/t соударений, сообщая всякий раз решетке энергию . Следовательно, в единице объема за единицу времени должно выделяться тепло
![]()
где n - число электронов проводимости в единице объема. Величина есть не что иное, как удельная мощность тока. Множитель при совпадает со значением (18.3) для закона Ома. Таким образом. Мы пришли к выражению закона Джоуля-Ленца в дифференциальной форме.
Теплоемкость металлов. Теплоемкость металла складывается из теплоемкости его кристаллической решетки и теплоемкости электронного газа. Поэтому атомная (т. е. рассчитанная на 1 моль) теплоемкость металла должна быть значительно большей, чем атомная теплоемкость диэлектриков, у которых нет свободных электронов. Согласно закону Дюлонга и Пти (см. §73), теплоемкость одноатомного кристалла равна 3R . Учтем, что теплоемкость одноатомного электронного газа равна 3 / 2 R . Тогда атомная теплоемкость металлов должна быть близка к 4,5R . Однако опыт доказывает, что она равна 3R, т. е. для металлов, так же как и для диэлектриков, хорошо выполняется закон Дюлонга и Пти. Следовательно, наличие электронов проводимости практически не сказывается на значении теплоемкости, что не объясняется классической электронной теорией.
Указанные расхождения теории с опытом можно объяснить тем, что движение электронов в металлах подчиняется не законам классической механики, а законам квантовой механики и, следовательно, поведение электронов проводимости надо описывать не статистикой Максвелла - Больцмана, а квантовой статистикой. Поэтому объяснить затруднения элементарной классической теории электропроводности металлов можно лишь квантовой теорией, которая будет рассмотрена в дальнейшем. Надо, однако, отметить, что классическая электронная теория не утратила своего значения и до настоящего времени, так как во многих случаях (например, при малой концентрации электронов проводимости и высокой температуре) она дает правильные качественные результаты и является по сравнению с квантовой теорией простой и наглядной.
Несамостоятельный и самостоятельный газовые разряды.
Несамостоятельный газовый разряд. Процесс прохождения электрического тока через газ называется газовым разрядом. Если электропроводность газа создается внешними ионизаторами, то электрический ток, возникающий в нем, называется несамостоятельным газовым разрядом. С прекращением действия внешних ионизаторов несамостоятельный разряд прекращается. Несамостоятельный газовый разряд не сопровождается свечением газа. Ниже изображен график зависимости силы тока от напряжения при несамостоятельном разряде в газе. Для построения графика использовалась стеклянная трубка с двумя впаянными в стекло металлическими электродами. Цепь собрана как показано на рисунке ниже.
|
|
Самостоятельный
газовый разряд.
Электрический разряд в газе, сохраняющийся после прекращения действия внешнего ионизатора, называется самостоятельным газовым разрядом . Для его осуществления необходимо, чтобы в результате самого разряда в газе непрерывно образовывались свободные заряды. Основным источником их возникновения является ударная ионизация молекул газа.
Если после достижения насыщения продолжать увеличивать разность потенциалов между электродами, то сила тока при достаточно большом напряжении станет резко возрастать (график 2).
Это означает, что в газе появляются дополнительные ионы, которые образуются за счет действия ионизатора. Сила тока может возрасти в сотни и тысячи раз, а число заряженных частиц, возникающих в процессе разряда, может стать таким большим, что внешний ионизатор будет уже не нужен для поддержания разряда. Поэтому ионизатор теперь можно убрать.
|
|
27. Магнитное поле, Магнитная индукция. Принцип суперпозиции магнитных полей. Закон Ампера.
Зако́н Ампе́ра - закон взаимодействия электрических токов . Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных - отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила , с которой магнитное поле действует на элемент объёма проводника с током плотности , находящегося в магнитном поле с индукцией :
![]() .
.
Модуль силы Ампера можно найти по формуле:
где - угол между векторами магнитной индукции и тока.
Сила максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции ():
Магни́тное по́ле - силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом , независимо от состояния их движения , магнитная составляющая электромагнитного поля
Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты ).
Магни́тная инду́кция - векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .
Более конкретно, - это такой вектор, что сила Лоренца , действующая со стороны магнитного поля на заряд , движущийся со скоростью , равна
![]()
где косым крестом обозначено векторное произведение , α - угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика ).
17.Сегнетоэлектрики - диэлектрики, которые обладают в определенном интервале температур спонтанной (самопроизвольной) поляризованностью, т. е. поляризованностью в условиях отсутствия внешнего электрического поля. К сегнетоэлектрикам относятся, например, подробно изученные И. В. Курчатовым (1903-1960) и П. П. Кобеко (1897-1954) сегнетова соль NaKC 4 H 4 O 6 4Н 2 O (от нее и было получено данное название) и титанат бария ВаТiO 3 .ПЬЕЗОЭЛЕКТРИКИ
кристаллические вещества, в к-рых при сжатии или растяжении в определённых направлениях возникает электрич. поляризация даже в отсутствии электрич. поля (п р я м о й п ь е з о э ф ф е к т). Следствием прямого пьезоэффектаявл. о б р а т н ы й п ь е з о э ф ф е к т - появление механич. деформации под действием электрич. поля. Связь между механич. и электрич. переменными (деформацией и электрич. полем) носит в обоих случаях линейный характер. Обратныйпьезоэффект следует отличать от электрострикции.
Пироэлектрики -кристаллическиедиэлектрики, обладающие самопроизвольной (спонтанной)поляризациейв отсутствие внешних воздействий. Обычно спонтанная поляризация не заметна, так как электрическое поле, создаваемое ею, компенсируется полем свободныхэлектрических зарядов, которые «натекают» на поверхность пироэлектрика из егообъёмаи из окружающеговоздуха. При изменении температуры величина спонтанной поляризации изменяется, что вызывает появление электрического поля, которое можно наблюдать до его компенсации свободными зарядами.
Диэлектрик (изолятор) - вещество, плохо проводящее или совсем не проводящее электрический ток. Плотность свободных носителей заряда в диэлектрике не превышает 108 шт/см³. Основное свойство диэлектрика состоит в способности поляризоваться во внешнем электрическом поле. Физическим параметром, который характеризует диэлектрик, является диэлектрическая проницаемость. Диэлектрическая проницаемость может иметь дисперсию. К диэлектрикам относятся воздух и другие газы, стекло, различные смолы, пластмассы непременно сухие. Химически чистая вода также является диэлектриком.
Развитие радиотехникипотребовало создания материалов, в которых специфические высокочастотные свойства сочетаются с необходимыми физико-механическими параметрами. Такие материалы называют высокочастотными. Для понимания электрических, магнитных и механических свойств материалов, а также причин старения нужны знания их химического и фазового состава, атомной структуры и структурных дефектов.
18.Электрическим током называют упорядоченное движение заряженных частиц или заряженных макроскопических тел. Различают два вида электрических токов – токи проводимости и конвекционные токи.
Током проводимости называют упорядоченное движение в веществе или вакууме свободных заряженных частиц – электронов проводимости (в металлах), положительных и отрицательных ионов (в электролитах), электронов и положительных ионов (в газах), электронов проводимости и дырок (в полупроводниках), пучков электронов (в вакууме). Этот ток обусловлен тем, что в проводнике под действием приложенного электрического поля напряженностью происходит перемещение свободных электрических зарядов.Конвекционным электрическим током называют ток, обусловленный перемещением в пространстве заряженного макроскопического тела Для возникновения и поддержания электрического тока проводимости необходимы следующие условия: 1) наличие свободных носителей тока (свободных зарядов); 2) наличие электрического поля, создающего упорядоченное движение свободных зарядов; 3) на свободные заряды, помимо кулоновских сил, должны действовать сторонние силы неэлектрической природы; эти силы создаются различными источниками тока (гальваническими элементами, аккумуляторами, электрическими генераторами и др.); 4) цепь электрического тока должна быть замкнутой. За направление электрического тока условно принимают направление движения положительных зарядов, образующих этот ток. Количественной мерой электрического тока является сила тока I - скалярная физическая величина, определяемая электрическим зарядом, проходящим через поперечное сечение S проводника в единицу времени:
Ток, сила и направление которого не изменяются с течением времени, называется постоянным Для постоянного тока
Электрический ток, изменяющийся с течением времени, называется переменным . Примером такого тока является синусоидальный электрический ток, применяемый в электротехнике и электроэнергетике (рис. 2.2, б ). Единица силы тока – ампер (А). В СИ определение единицы силы тока формулируется следующим образом: 1А – это сила такого постоянного тока, который при протекании по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, создает между этими проводниками силу, равную на каждый метр длины. Для характеристики направления электрического тока проводимости в разных точках поверхности проводника и распределения силы тока по этой поверхности вводится плотность тока.Плотностью тока называют векторную физическую величину, совпадающую с направлением тока в рассматриваемой точке и численно равную отношению силы тока dI , проходящего через элементарную поверхность, перпендикулярной направлению тока, к площади этой поверхности:
Единица плотности тока – ампер на квадратный метр (А/м2 ). Плотность постоянного электрического тока одинакова по всему поперечному сечению однородного проводника. Поэтому для постоянного тока в однородном проводнике с площадью поперечного сечения S сила тока равна
Если в цепи на носители тока действуют только силы электростатического поля, то происходит перемещение зарядов от точек с большим потенциалом к точкам с меньшим потенциалом. Это приводит к выравниванию потенциалов во всех точках цепи и к исчезновению тока. Поэтому для поддержания постоянного электрического тока в цепи необходимо наличие устройства, способного создавать и поддерживать разность потенциалов за счет работы некоторых сторонних сил. Такие устройства называют источниками тока . Под действием сторонних сил носители тока движутся внутри источника электрической энергии против сил электростатического поля (против кулоновских сил, вызывающих соединение разноименных зарядов, а следовательно, выравнивание потенциалов и исчезновение тока), так что на концах внешней цепи поддерживается постоянная разность потенциалов и в цепи протекает постоянный электрический ток. Сторонние силы совершают работу по перемещению электрических зарядов. Физическая величина, определяемая работой сторонних сил при перемещении единичного положительного заряда, называется электродвижущей силой (ЭДС) источника: Единица ЭДС –вольт (В). Сторонняя сила, действующая на заряд , может быть выражена через напряженностьполя сторонних сил
Тогда работа сторонних сил по перемещению заряда на замкнутом участке цепи будет равна:
![]()
Разделив на и учитывая (получим выражение для ЭДС, действующей в цепи:
19.Последовательное и параллельное соединения вэлектротехнике- два основных способа соединения элементовэлектрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одногоузла. При параллельном соединении все входящие в цепь элементы объединены двумяузламии не имеют связей с другими узлами, если это не противоречит условию.
При последовательном соединении проводников сила тока во всех проводниках одинакова.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Последовательное соединение
При последовательном соединении проводников сила тока в любых частях цепи одна и та же:
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:
Резисторы
Катушка индуктивности
Электрический конденсатор
.
Параллельное соединение
Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединённых проводниках:
Напряжение на участках цепи АВ и на концах всех параллельно соединённых проводников одно и то же:
Резистор
При параллельном соединении резисторов складываются величины, обратно пропорциональные сопротивлению (то есть общая проводимость складывается из проводимостей каждого резистора)
![]()
Если цепь можно разбить на вложенные подблоки, последовательно или параллельно включённые между собой, то сначала считают сопротивление каждого подблока, потом заменяют каждый подблок его эквивалентным сопротивлением, таким образом находится общее(искомое) сопротивление.
Для
двух параллельно соединённых резисторов
их общее сопротивление равно:
![]() .
.
Если , то общее сопротивление равно:
При параллельном соединении резисторов их общее сопротивление будет меньше наименьшего из сопротивлений.
Катушка индуктивности
![]()
Электрический конденсатор
Закон Ома для участка цепи. Немецкий физик Георг Ом (1787-1854) в 1826 г. обнаружил, что отношение напряженияU между концами металлического проводника, являющегося участком электрической цепи, к силе токаI в цепи есть величина постоянная:
Эту величину R называютэлектрическим сопротивлением проводника. Единица электрического сопротивления в СИ -ом (Ом). Электрическим сопротивлением 1 Ом обладает такой участок цепи, на котором при силе тока 1 А напряжение равно 1 В:
Опыт показывает, что электрическое сопротивление проводника прямо пропорционально его длине l и обратно пропорционально площадиS поперечного сечения:
Постоянный для данного вещества параметр называетсяудельным электрическим сопротивлением вещества. Экспериментально установленную зависимость силы токаI от напряженияU и электрического сопротивленияR участка цепи называютзаконом Ома для участка цепи:
Закон Джоуля-Ленца формула и формулировка
Так или иначе, оба ученых исследовали явление нагревания п роводников электрическим током, они установили опытным путём следующую закономерность: количество теплоты, которое выделяется в проводнике с током, прямо пропорционально сопротивлению проводника, квадрату силы тока и времени прохождения тока.
Позже дополнительные исследования выявили, что данное утверждение справедливо для всех проводников: жидких, твёрдых и даже газообразных. В связи с этим открытая закономерность стала законом.
Итак, рассмотрим сам закон Джоуля-Ленца и его формулу, которая выглядит так:
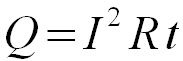
20. Электродвижущая сила (ЭДС) - скалярнаяфизическая величина , характеризующая работу сторонних (непотенциальных) сил висточниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равнаработе этих сил по перемещению единичного положительногозаряда вдоль контура.
ЭДС можно выразить через напряжённость электрического поля сторонних сил (). В замкнутом контуре () тогда ЭДС будет равна:
![]() ,
где
-
элемент длины контура.
,
где
-
элемент длины контура.
ЭДС так же, как и напряжение , измеряется в вольтах . Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого источника равна нулю.
Баланс мощностей Для любых замкнутых цепей сумма мощностей источников электрической энергии Р И, равна сумме мощностей, расходуемых в приемниках энергии Р П. Мощность источников указывает на то, какое количество работы они могут выполнить в электрической цепи каждую секунду. Максимально допустимая мощность приемников это то, что в нормальных условиях может выдержать пассивный элемент. Если превысить допустимую мощность резисторов, обычно указываемую на корпусе, то он может перегреться, его проводящий слой разрушится, почернеет окраска корпуса и деталь выйдет из строя.
Мощность, отдаваемая источниками ЭДС, равна.
Общее количество теплоты, выделяемое током в цепи, не всегда совпадает с соответствующим джоулевым теплом. Так на месте контакта двух различных проводников, помимо джоулева тепла, выделяется также, так называемое тепло Пельтье, зависящее от сторонних ЭДС, определяемых в свою очередь химической природой проводников, их температурой и т.д. При наличии в проводнике градиента температур в нем выделяется еще и теплота Томсона. В большинстве практических случаев при небольших токах теплотой Пельтье и Томсона можно пренебрегать.
Пра́вилазна́ков (в оптике) - правила определения знаков величин и направлений, принятые при расчёте оптических систем, а также при изображении (и чтении) оптических схем.
При расчёте и анализе оптических систем, положительным направлением (прямым ходом луча) вдоль оптической оси считается направление света слева направо, преломляющие и отражающие поверхности и разделяющие их среды нумеруются по порядку их следования в направлении распространения света, а оптическую систему принято изображать так, чтобы её первая (входная) поверхность располагалась на рисунке (чертеже, схеме) слева.
К тому же, при расчёте принято придерживаться некоторых правил, которые, так же, отражаются на схемах, чертежах и рисунках:
угол луча с оптической осью считается положительным, если луч, пересекающий ось, идёт сверху вниз, и отрицательным, если снизу вверх;
линейные величины предмета и изображения, а также отрезки высот лучей считаются положительными, если они расположены над осью, и отрицательными, если под нею;
радиус кривизны поверхности считается положительным, если её центр находится справа от поверхности, и отрицательным - если слева от поверхности, то есть отсчёт производится от поверхности к центру;
величины толщин и воздушных промежутков между преломляющими поверхностями при движении света слева направо всегда считаются положительными;
углы между лучом и нормалью к поверхности в точках падения луча ε и ε" (углы падения и преломления) считаются положительными, если нормаль , чтобы совпасть с направлением луча, должна быть повёрнута по ходу часовой стрелки;
угол φ между нормалью и оптической осью считается положительным, если оптическая ось, чтобы совпасть с нормалью, должна быть повёрнута по ходу часовой стрелки;
при отражении на поверхности изменяется знак у показателя преломления n", угла отражения ε" и величины расстояния между отражающей поверхностью и следующей (при движении света справа налево);
фокусные расстояния считаются положительными по направлению света от главных плоскостей ;
при преломлении и отражении лучей на сферической поверхности за начало отсчёта отрезка принимается вершина поверхности (точка 0 ). Отрезки считаются положительными, если они откладываются вдоль оси справа от точки 0 по направлению распространения света, и отрицательными, когда откладываются слева от точки 0 . В случае отрицательных значений указанных величин перед ними ставится знак минус.
Одноимённые (соответственные) и сопряжённые точки, отрезки и углы в пространстве предметов и пространстве изображений обозначаются одинаковыми буквами. Исключение, здесь, делается для точек переднего F и заднего F" фокусов которые обозначаются одинаковой буквой хотя и не сопряжены друг с другом.
Обозначения относящиеся к пространству изображений, обозначаются знаком "штрих" сверху каждой буквы. Например, обозначение задней главной плоскости указывает, что данная плоскость принадлежит, именно, пространству изображений.
22.Правила Кирхгофа (часто, в литературе, называются не совсем корректноЗако́ныКирхго́фа ) - соотношения, которые выполняются между токами и напряжениями на участках любойэлектрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного иквазистационарного тока. Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач втеории электрических цепейи практических расчётов сложных электрических цепей. Применение правил Кирхгофа к линейной электрической цепи позволяет получитьсистему линейных уравненийотносительно токов или напряжений, и соответственно, найти значение токов на всех ветвях цепи и все межузловые напряжения. СформулированыГуставом Кирхгофомв1845 году. Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами Природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (3-еуравнение Максвеллапри неизменном магнитном поле).
Опытом установлено, что если в проводнике течет ток, то работа сторонних сил расходуется на его нагревание. Предположим, что на концах участка проводника имеется разность потенциалов U = φ 1 – φ 2 .
Тогда работа по переносу заряда Q на этом участке равна
A = Q (φ 1 – φ 2) = QU.
Если ток постоянный, то
A = I · U · t.
Эта работа равна количеству теплоты Q, и формула Q = I · U · t выражает закон Джоуля-Ленца в интегральной форме.
Используя выражение закона Ома получим
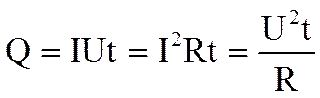 .
.
Преобразуем закон Джоуля–Ленца. Введем плотность тепловой мощности w – величину, равную энергии, выделяемой за время t прохождения тока в единице объема проводника:
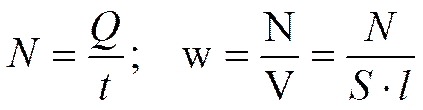
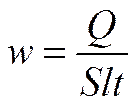 ,
,
где S - сечение, l
- длина проводника. Подставляя Q = I 2 R t и  , получим
, получим 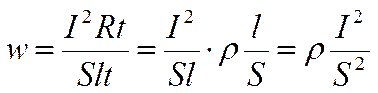 .
.
Здесь - плотность тока, , и учитывая, что j = γE, получим
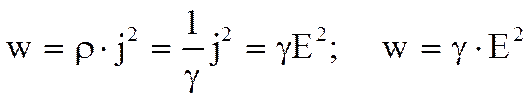 .
.
Это есть выражение закона Джоуля-Ленца в дифференциальной форме. Плотность тепловой мощности в проводнике, по которому течет ток, прямо пропорциональна квадрату напряженности поля в проводнике. Коэффициентом пропорциональности является удельная проводимость проводника.
Вывод законов Ома и Джоуля-Ленца из классических электронных представлений
Какова природа носителей тока в металлах? В 1901 г. Рикке проделал опыты: через 3 цилиндра, установленных друг на друга в течение 3-х лет пропускал постоянный ток. Был пропущен заряд, равный 3,5 ·10 6 Кл. Взвешивание показало неизменный вес цилиндров. Исследование торцов цилиндров не показало следов переноса вещества. Из этого был сделан вывод, что носители заряда не ионы, а открытые Томпсоном в 1897 г. электроны.
Чтобы отождествить носители заряда с электронами, нужно было определить знак и величину удельного заряда носителей.
Если в металле имеются легко перемещающиеся заряженные частицы, то при торможении металлического проводника эти частицы должны некоторое время продолжать двигаться по инерции, в результате чего в проводнике возникнет импульс тока и будет перенесен некоторый заряд.
Мандельштам и Папалекси в 1913 г. проделали такой опыт – они приводили в быстрое крутильное колебание катушку с проводом вокруг ее оси. К концам катушки подключили телефон, в котором был слышен звук, обусловленный импульсами тока. Был получен качественный результат – зарегистрирован импульс тока.
Толмен и Стюарт в 1916 г. получили количественный результат. Катушка с проводом длиной 500 м приводилась во вращение со скоростью v=300 м/с. Катушка резко тормозилась и с помощью баллистического гальванометра измеряли заряд, протекавший в цепи во время торможения. Вычисленное значение отношения заряда к массе e/m получалось очень близким для электронов. Таким образом было доказано, что носителем тока являются электроны. Исходя из представлений о свободных электронах была создана классическая теория электропроводности металлов в предположении, что:
Электроны в металле ведут себя подобно молекулам идеального газа;
Движение электронов подчиняется законам классической механики;
Взаимодействие электронов сводится к соударениям с ионами кристаллической решетки;
Силами взаимодействия между электронами можно пренебречь и они между собой не сталкиваются;
Электроны в отсутствие электрического поля движутся хаотически.
Вычислим плотность тока j в проводнике, возникающего под действием поля напряженностью Е.
По определению плотность тока j = n·e·
На каждый электрон действует сила F = eE = ma, поэтому электрон приобретает ускорение и к концу свободного пробега он достигнет скорости
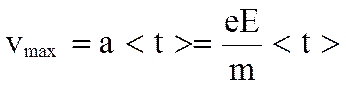 , а средняя скорость
, а средняя скорость
Если
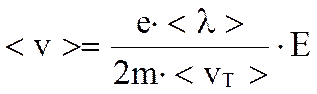 .
.
Подставляя
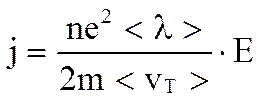 ,
,
т.е. плотность тока прямо пропорциональна Е, а это и есть выражение закона Ома в дифференциальной форме. Если положить, что
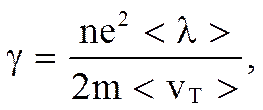 то
то
j = γ E .
Удельная проводимость γ ~ n и < λ>, 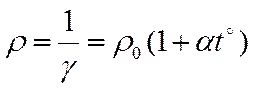 повышается с ростом температуры. К концу свободного пробега электрон приобретает кинетическую энергию
повышается с ростом температуры. К концу свободного пробега электрон приобретает кинетическую энергию
Предполагается, что вся энергия при соударении передается узлу кристаллической решетки и переходит в тепло. За 1 с электрон испытывает
Таким образом, 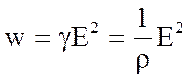 - выражение закона Джоуля-Ленца в дифференциальной форме.
- выражение закона Джоуля-Ленца в дифференциальной форме.
Закон Видемана-Франца. Затруднения классической электронной теории
Известно, что металлы наряду с высокой электропроводностью обладают также большой теплопроводностью. Видеман и Франц в 1853 г. эмпирически установили закон: отношение коэффициента теплопроводности χ к коэффициенту электропроводности γ для всех металлов приблизительно одинаково и прямо пропорционально абсолютной температуре
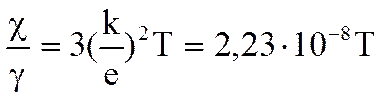 .
.
Таким образом, классическая электронная теория хорошо объясняет существование электрического сопротивления металлов, законы Ома и Джоуля-Ленца, позволяет выразить удельную теплопроводность через атомарные постоянные металла, объясняет зависимость электропроводности от температуры и позволяет понять связь между теплопроводностью и электропроводностью металлов.
Однако в некоторых вопросах, классическая электронная теория приходит к выводам, находящимся в противоречии с опытом.
1. Исходя из классической электронной теории удельная электропроводность равна
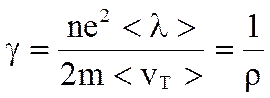 ,
,
 , но
, но  ,
,
т.е.
Следовательно, по теории ρ ∼ , тогда как на практике
т.е. удельное сопротивление пропорционально первой степени температуры Т.
Кроме того, согласно классической электронной теории удельное сопротивление ρ должно монотонно уменьшаться при охлаждении, оставаясь при всех температурах по значению конечным. Это и наблюдается при сравнительно высоких температурах. Однако при достаточно низких температурах удельное сопротивление перестает зависеть от температуры и достигает некоторого предельного значения, которое называют остаточным сопротивлением (велико у сплавов, существует у чистых металлов и тем меньше, чем чище металл и меньше структурных дефектов).
Если понижать температуру еще ниже, то в некоторых веществах наблюдается явление сверхпроводимости, т.е. удельное сопротивление внезапно скачком уменьшается практически до нуля (рис. 96). В сверхпроводниках однажды возбужденный электрический ток может длительно существовать без источника тока (в течение нескольких суток). В таком состоянии не выполняется закон Ома.
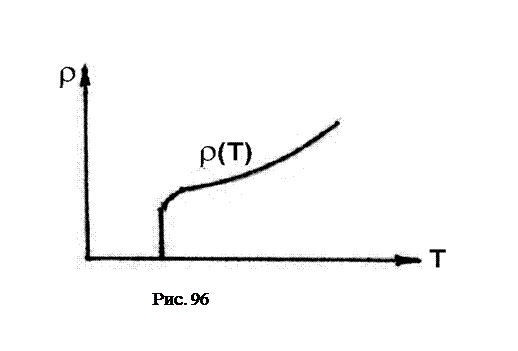
2. Другим затруднением классической электронной теории металлов может служить теория теплоемкости кристаллов. Согласно этой теории “электронный газ” металлов должен обладать молярной теплоемкостью . Добавляя эту теплоемкость к теплоемкости кристаллической решетки, составляющей 3R, получим для молярной теплоемкости металла значение (9/2)R. Таким образом, согласно классической электронной теории молярная теплоемкость металла должна быть в 1,5 раза выше, чем у диэлектриков. Однако на практике их молярные теплоемкости практически не различаются. Объяснение этих различий и явлений дается в рамках квантовой теории металлов.
В классической теории неверным является предположение, что электроны проводимости подчиняются законам статистики Максвелла-Больцмана и что для них справедлив закон распределения энергии Максвелла. На самом деле они подчиняются законам квантовой статистики и закону распределения энергий Ферми-Дирака.
Энергия электронов в металлах слабо зависит от температуры и теплоемкость электронного газа оказывается близка к нулю, поэтому наличие электронного газа в металлах практически не сказывается на теплоемкости.
Далее, в классической электронной теории не учитывается взаимодействие электронов друг с другом, а их взаимодействие с решеткой металла описывается с помощью представления о соударениях. При низких температурах взаимодействие между электронами начинает играть решающую роль. Кроме того, оказалось, что взаимодействие электронов с решеткой имеет иной характер – электроны движутся в периодическом поле электрического потенциала решетки.
И, наконец, движение электронов в металлах подчиняется законам квантовой , а не классической механики.