Теорема Гаусса позволяет в ряде случаев найти напряженность поля гораздо более простыми средствами, чем с использованием формулы (5.3) для напряженности поля точечного заряда и принципа суперпозиции полей.
Продемонстрируем возможности теоремы Гаусса на нескольких полезных для дальнейшего примерах. Прежде чем приступить к рассмотрению этих примеров, введем понятия поверхностной и линейной плотностей заряда.
Если заряд сосредоточен в тонком поверхностном слое несущего заряд тела, распределение заряда в пространстве можно охарактеризовать с помощью поверхностной плотности о, которая определяется выражением
Здесь - заряд, заключенный в слое площади Под подразумевается физически бесконечно малый участок поверхности.
Если заряд распределен по объему или поверхности цилиндрического тела (равномерно в каждом сечении), используется линейная плотность заряда
Длина физически бесконечно малого отрезка цилиндра, заряд, сосредоточенный на этом отрезке).
Поле бесконечной однородно заряженной плоскости.
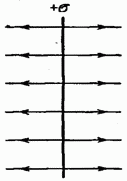
Пусть поверхностная плотность заряда во всех точках плоскости одинакова и равна а; для определенности будем считать заряд положительным. Из соображений симметрии вытекает, что напряженность поля в любой точке имеет направление, перпендикулярное к плоскости. Действительно, поскольку плоскость бесконечна и заряжена однородно, нет никаких оснований к тому, чтобы вектор Е отклонялся в какую-либо сторону от нормали к плоскости. Далее очевидно, что в симметричных относительно плоскости точках напря-. женность поля одинакова по величине и противоположна по направлению.
Представим себе мысленно цилиндрическую поверхность с образующими, перпендикулярными к плоскости, и основаниями величины , расположенными относительно плоскости симметрично (рис. 14.1). В силу симметрии Применим к поверхности теорему Гаусса. Поток через боковую часть поверхности будет отсутствовать, поскольку в каждой ее точке равна нулю. Для оснований совпадает с Е. Следовательно, суммарный поток через поверхность равен Внутри поверхности заключен заряд a . Согласно теореме Гаусса должно выполняться условие
![]()
из которого
Полученный нами результат не зависит от длины цилиндра. Это означает, что на любых расстояниях от плоскости напряженность поля одинакова по величине. Вид линий напряженности показан на рис. 14.2. Для отрицательно заряженной плоскости результат будет таким же, лишь направление вектора Е и линий напряженности изменится на обратное.

Если взять плоскость конечных размеров, например заряженную тонкую пластинку то полученный выше результат будет справедливым только для точек, расстояние которых от края пластинки значительно превышает расстояние от самой пластинки (на рис. 14.3 область этих точек обведена пунктирной кривой).
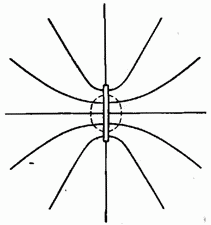
По мере удаления от плоскости или приближения к ее краям поле будет все больше отличаться от поля бесконечной заряженной плоскости.
Характер поля на больших расстояниях легко представить, если учесть, что на расстояниях, значительно превышающих размеры пластинки, создаваемое ею поле можно рассматривать как поле точечного заряда.
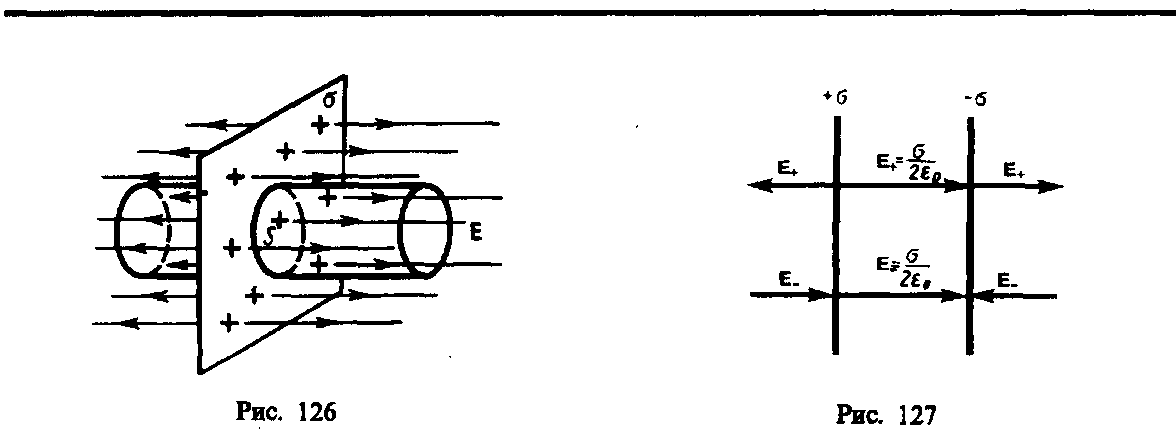
1. Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость (рис. 126) заряжена с постояннойповерхностной плотностью +s(s= dQ/ dS - заряд, приходящийся на единицу поверхности). Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (соsa=0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равенсумме потоков сквозь его основания (площади оснований равны и для основания Е n совпадает с Е ), т. е. равен 2ES. Заряд, заключенный внутри построенной цилиндрической поверхности, равен sS. Согласно теореме Гаусса (81.2), 2ES= sS/ e 0 , откуда
Из формулы (82.1) вытекает, что Е не зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно.
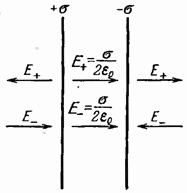
2. Поле двух бесконечных параллельных разноименно заряженных плоскостей (рис. 127). Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями + sи –s. Поле таких плоскостей найдемкак суперпозицию полей, создаваемых каждой из плоскостей в отдельности. На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние - от отрицательной плоскости. Слева и справа от плоскостей поля вычитаются (линии напряженности направлены навстречу друг другу), поэтому здесь напряженность поля E =0. В области между плоскостями E = E + + E – (E + и E – определяются по формуле (82.1)), поэтому результирующая напряженность
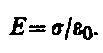 (82.2)
(82.2)
Таким образом, результирующая напряженность поля в области между плоскостями описывается формулой (82.2), а вне объема, ограниченного плоскостями, равна нулю.
3. Поле равномерно заряженной сферической поверхности.
Сферическая поверхность радиуса R с
общим зарядом Q
заряжена равномерно с поверхностной плотностью +s. Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией. Поэтому линии напряженности направлены радиально (рис. 128). Построим мысленно сферу радиуса r,
имеющую общий центр с заряженной сферой. Если r>R,ro
внутрь поверхности попадает весь заряд Q,
создающий рассматриваемое поле, и, по теореме Гаусса (81.2), 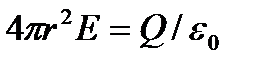 ,
откуда
,
откуда
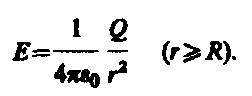 (82.3)
(82.3)
При r>R
поле убывает с расстоянием r
по такому же закону,как у точечного заряда. График зависимости Е
от r
приведен на рис. 129. Если r"
4. Поле объемно заряженного шара. Шар радиуса R с общим зарядом Q заряжен равномерно собъемной плотностью r(r = –заряд, приходящийся на единицу объема). Учитывая соображения
симметрии (см. п. 3), можно показать, что для напряженности поля вне шара получится тот же результат, что и в предыдущем случае (см. (82.3)). Внутри же шара напряженность поля будет другая. Сфера радиуса r"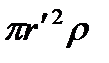 .
Поэтому, согласно теореме Гаусса (81.2), . Учитывая, что
.
Поэтому, согласно теореме Гаусса (81.2), . Учитывая, что 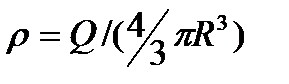 ,
получаем
,
получаем
 (82.4)
(82.4)
Таким образом, напряженность поля вне равномерно заряженного шара описывается формулой (82.3), а внутри его изменяется линейно с расстоянием r" согласно выражению (82.4). График зависимости Е от r для рассмотренного случая приведен на рис. 130.
5. Поле равномерно заряженного бесконечного цилиндра (нити). Бесконечный цилиндр радиуса R (рис. 131) заряжен равномерно слинейной плотностью t (t = – заряд, приходящийся на единицу длины). Из соображений симметрии следует, что линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим коаксиальный с заряженным цилиндр радиуса r и высотой l . Поток вектора Е сквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность равен 2prlЕ. По теореме Гаусса (81.2), при r>R 2prlЕ = tl/e 0 , откуда
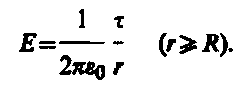 (82.5)
(82.5)
Если r
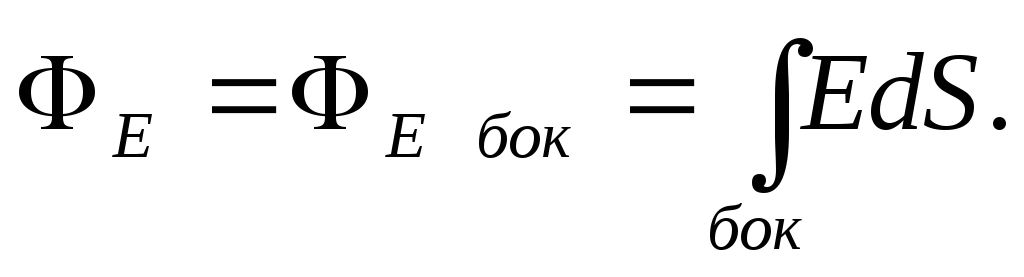
Очевидно, на одинаковом
расстоянии r
от нити значения Е
будут одинаковы, поэтому
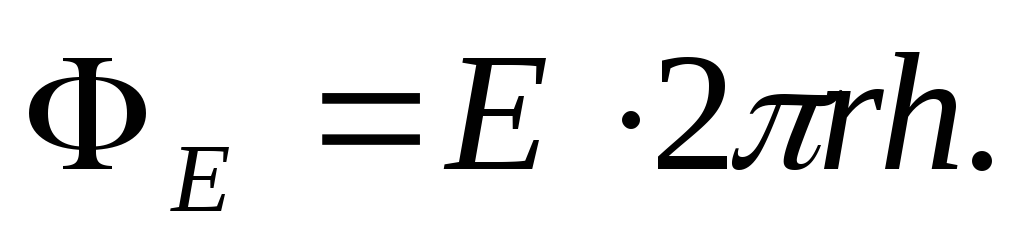 Согласно теореме Гаусса
Согласно теореме Гаусса
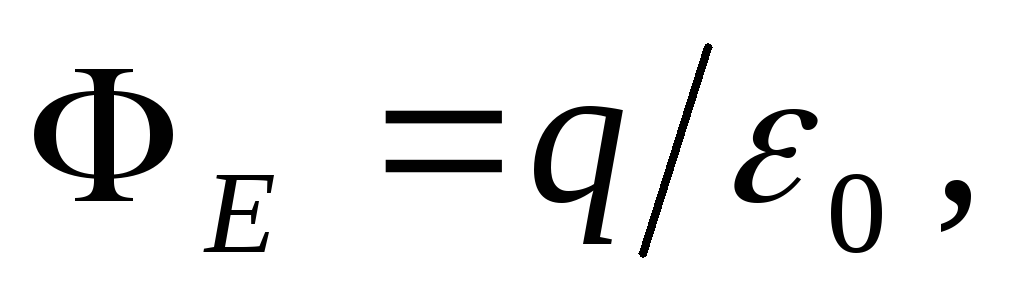
где
 -
заряд, заключенный внутри гауссова
цилиндра. Тогда
-
заряд, заключенный внутри гауссова
цилиндра. Тогда
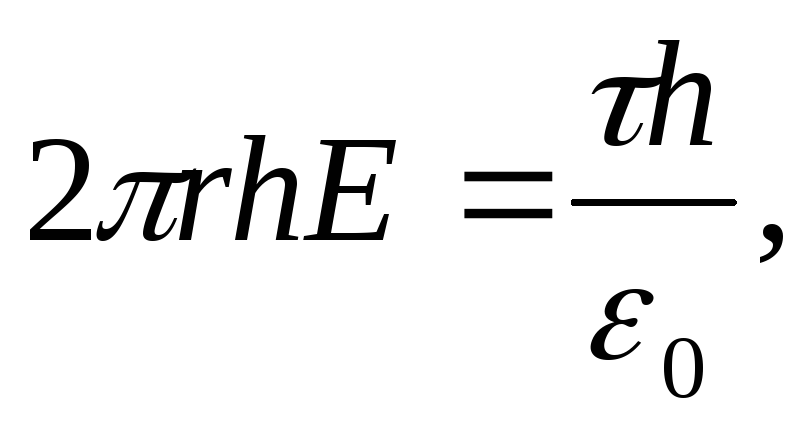
и
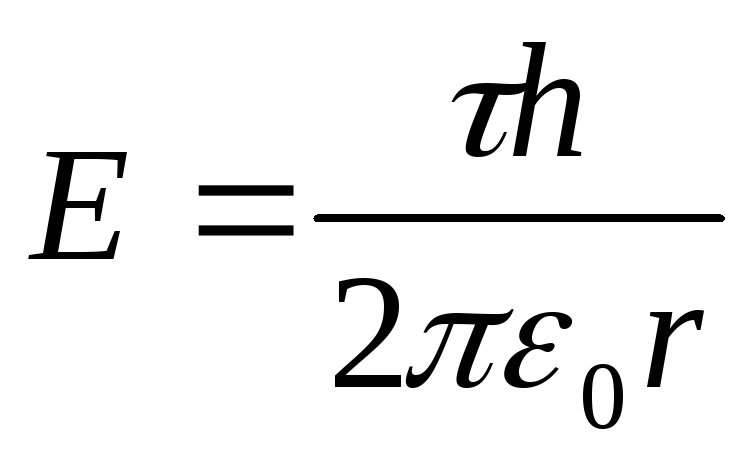 - напряженность поля заряженной нити
на расстоянииr
от нее.
- напряженность поля заряженной нити
на расстоянииr
от нее.
2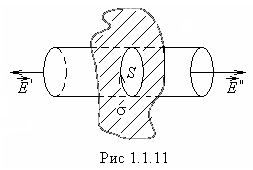 .
Поле бесконечной однородной заряженной
плоскости. Поверхностная плотность
заряда
.
Поле бесконечной однородной заряженной
плоскости. Поверхностная плотность
заряда во всех точках плоскости одинакова
во всех точках плоскости одинакова .
Напряженность поля перпендикулярна к
плоскости. В симметричных относительно
плоскости точках напряженность поля
одинакова по величине и противоположна
по направлению. Построим цилиндрическую
поверхность с образующими, перпендикулярными
к плоскости, и основаниями
.
Напряженность поля перпендикулярна к
плоскости. В симметричных относительно
плоскости точках напряженность поля
одинакова по величине и противоположна
по направлению. Построим цилиндрическую
поверхность с образующими, перпендикулярными
к плоскости, и основаниями (рис.1.1.11). В силу симметрии
(рис.1.1.11). В силу симметрии .
.
П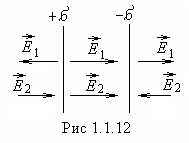 оток
через боковую поверхность
равен нулю, так как вектор
оток
через боковую поверхность
равен нулю, так как вектор перпендикулярен к этой поверхности,
таким образом суммарный поток через
поверхность цилиндра равен
перпендикулярен к этой поверхности,
таким образом суммарный поток через
поверхность цилиндра равен ,
и
,
и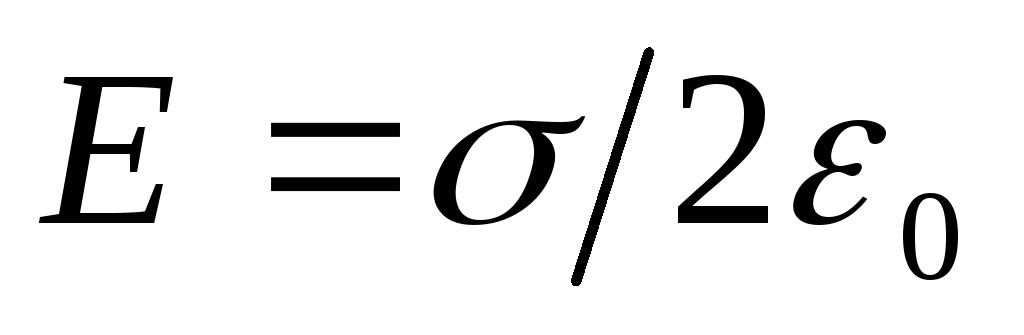 .
.
3.Рассмотрим электрическое
поле, созданное двумя разноименно
заряженными плоскостями с поверхностными
плотностями заряда
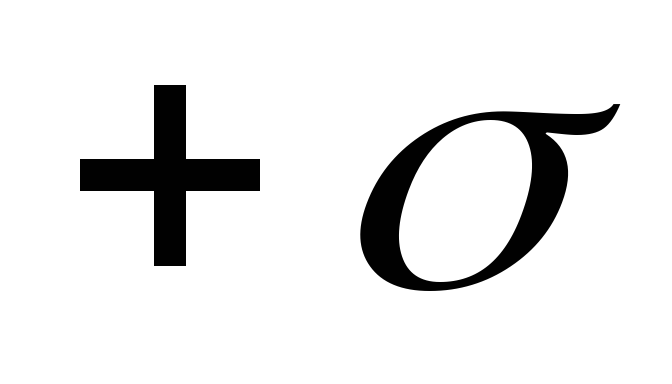 и
и .
Очевидно, напряженности полей плоскостей
направлены в одну сторону (от положительной
плоскости к отрицательной, рис.1.1.12), и
р
.
Очевидно, напряженности полей плоскостей
направлены в одну сторону (от положительной
плоскости к отрицательной, рис.1.1.12), и
р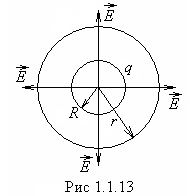 езультирующая
напряженность
езультирующая
напряженность ,
где
,
где - напряженность поля одной заряженной
плоскости. Окончательно получаем
- напряженность поля одной заряженной
плоскости. Окончательно получаем
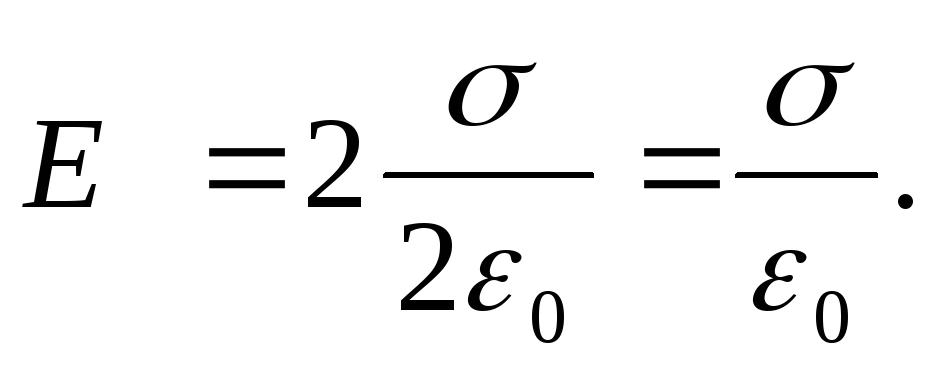
4.Вычислим напряженность
электрического поля, создаваемого
заряженной сферой радиуса R
.
Заряд сферы q
,
его поверхностная плотность
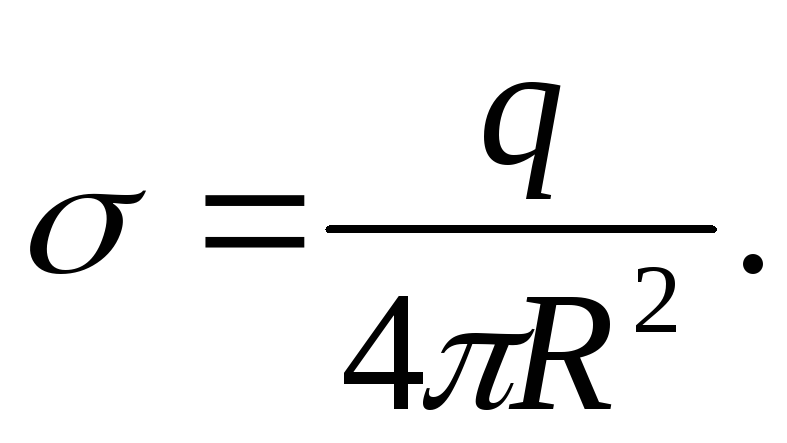 Для определения напряженности построим
гауссову поверхность в виде сферы
радиусаr
,
центр которой совпадает с центром
заряженной сферы (рис.1.1.13).
Для определения напряженности построим
гауссову поверхность в виде сферы
радиусаr
,
центр которой совпадает с центром
заряженной сферы (рис.1.1.13).
 Приr
≤
R
внутри гауссовой
поверхности зарядов нет, так как весь
заряд распределен по поверхности сферы.
По теореме Гаусса
Приr
≤
R
внутри гауссовой
поверхности зарядов нет, так как весь
заряд распределен по поверхности сферы.
По теореме Гаусса
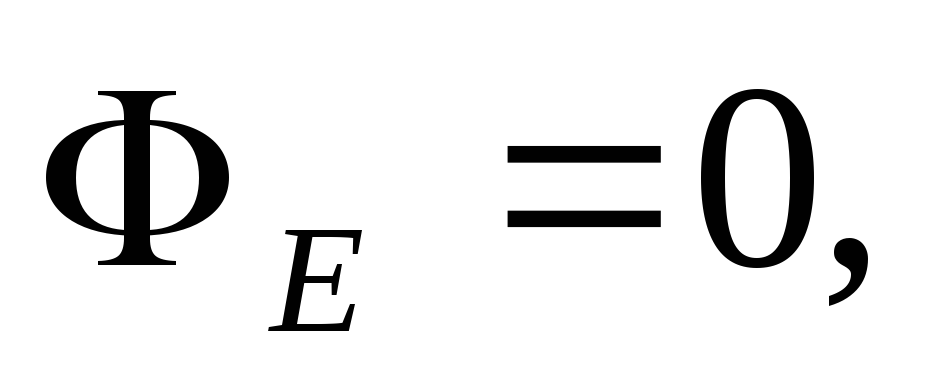 или
или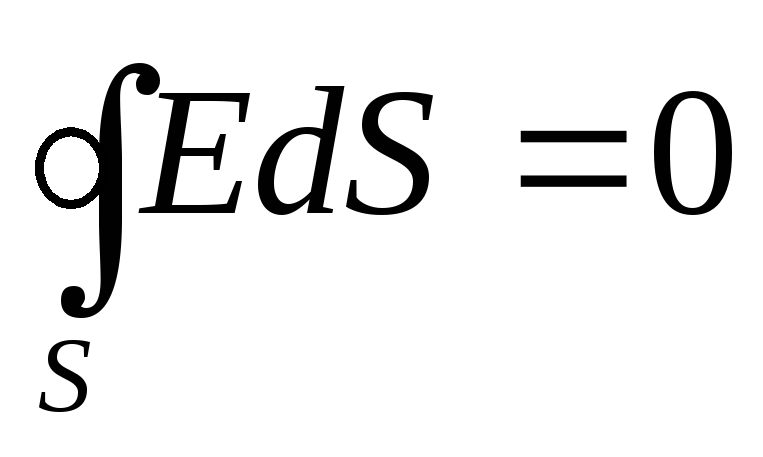 ,
следовательно,
,
следовательно,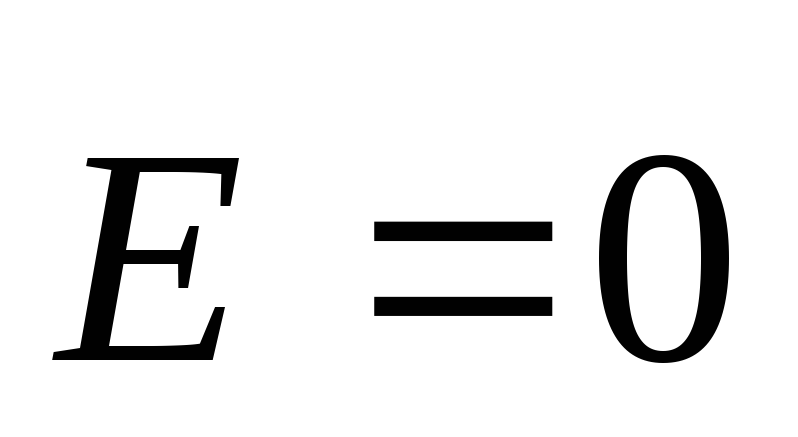 - напряженность электрического поля
внутри заряженной сферы равна нулю.
- напряженность электрического поля
внутри заряженной сферы равна нулю.
 При
При
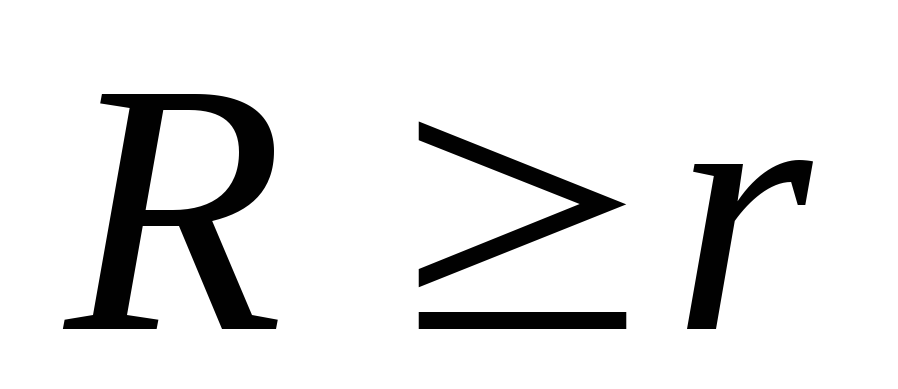 внутрь гауссовой
поверхности попадает весь заряд q
сферы. В силу центральной симметрии
поля напряженность на расстоянии r
от центра сферы всюду одинакова, и
внутрь гауссовой
поверхности попадает весь заряд q
сферы. В силу центральной симметрии
поля напряженность на расстоянии r
от центра сферы всюду одинакова, и
 или
или при этом
при этом ,
тогда,
и
,
тогда,
и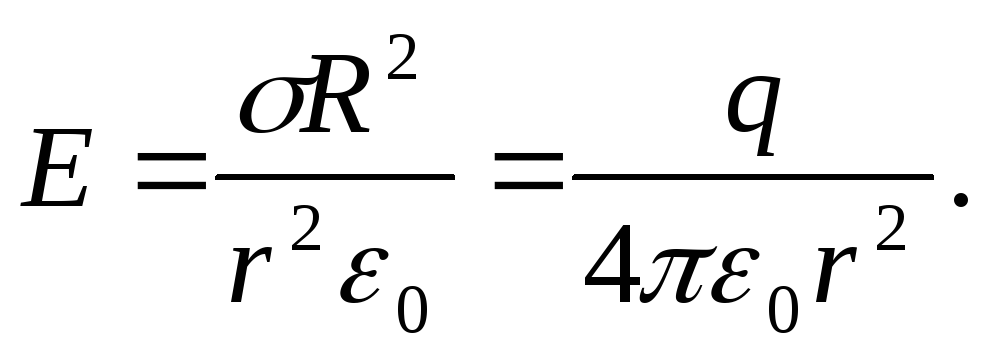 С ростомr
значения Е
убывают
пропорционально
С ростомr
значения Е
убывают
пропорционально
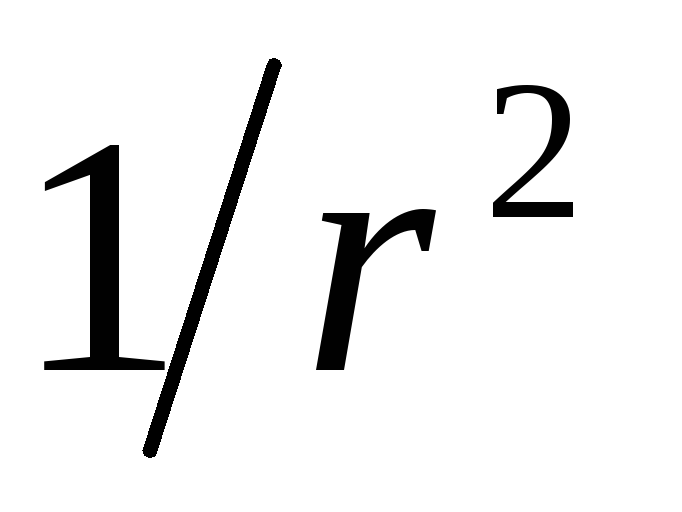 (рис.1.1.14). На поверхности
сферы напряженность испытывает скачек
(рис.1.1.14). На поверхности
сферы напряженность испытывает скачек

5.Рассмотрим электрическое поле, созданное объемно заряженным шаром радиуса R . Объемная плотность заряда шара ρ. Гауссову поверхность построим в виде сферы, центр которой совпадает с центром шара, а радиус равен r (рис.1.1.15).
При
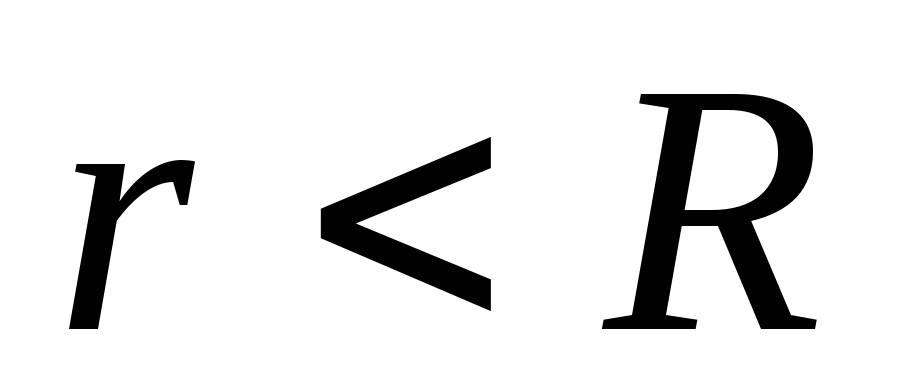 внутрь гауссовой
поверхности попадает заряд
внутрь гауссовой
поверхности попадает заряд
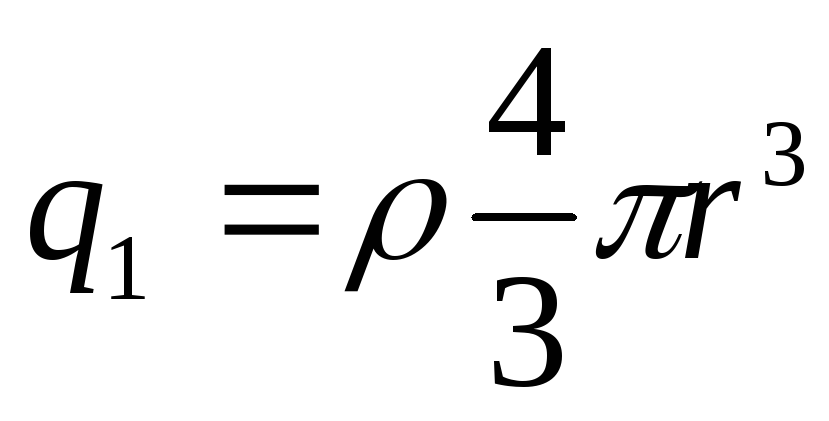 ,
тогда по теореме Гаусса
,
тогда по теореме Гаусса
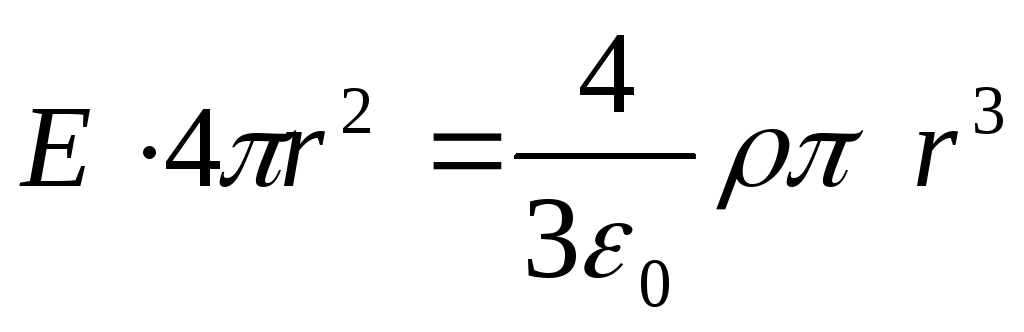 ,
и
,
и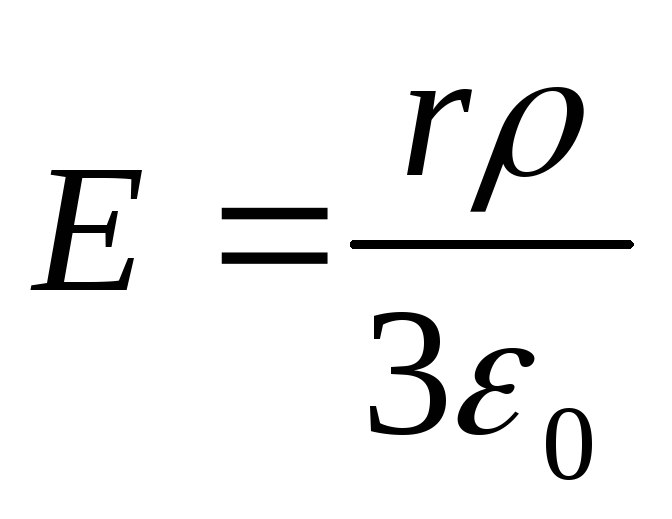 .
На поверхности шара приr
=
R
напряженность
.
На поверхности шара приr
=
R
напряженность
 .
.
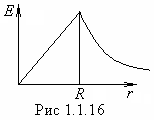 При
При внутрь гауссовой поверхности попадает
весь заряд
внутрь гауссовой поверхности попадает
весь заряд ,
и
,
и ,
отсюда
,
отсюда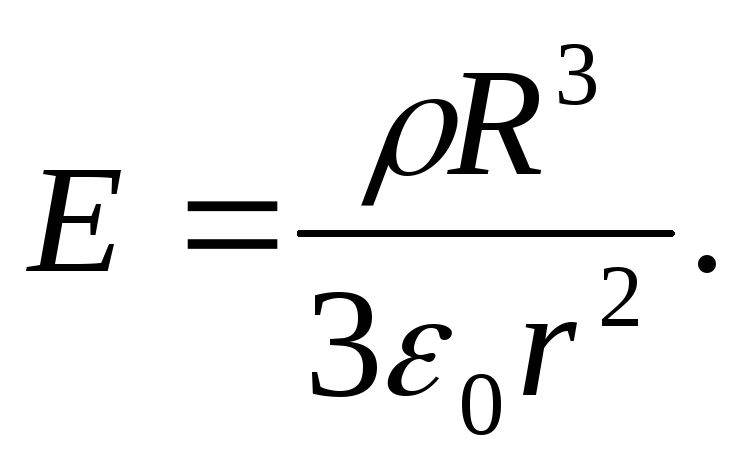 На поверхности сферы
На поверхности сферы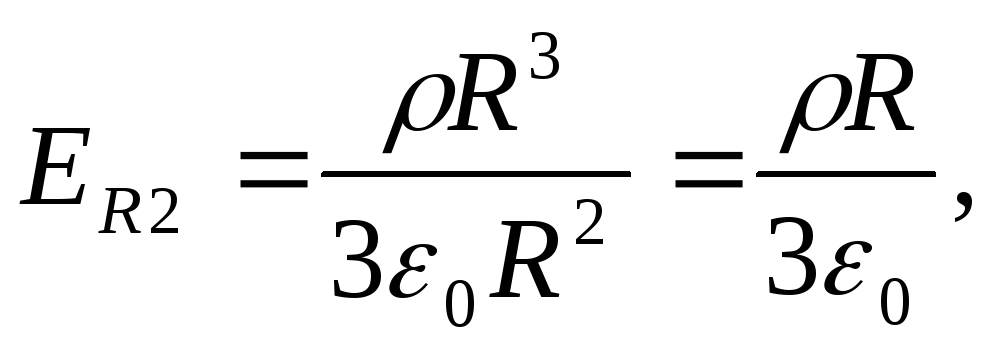 т.е.
т.е.![]() и скачка напряженности не происходит.
Зависимость
и скачка напряженности не происходит.
Зависимость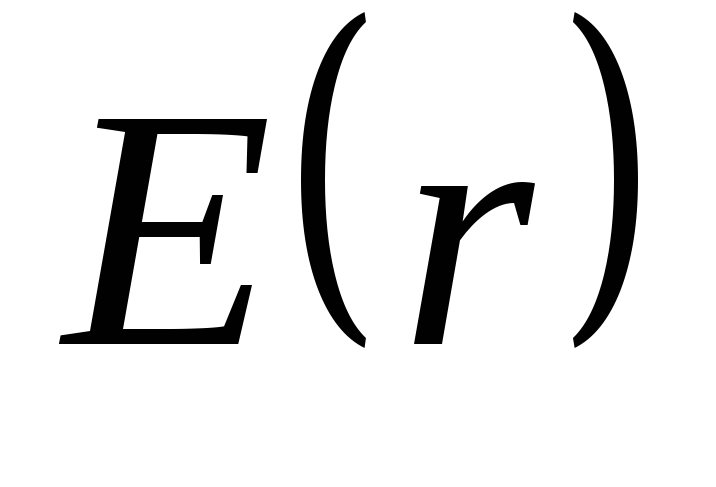 представлена на рис1.1.16.
представлена на рис1.1.16.
Лекция 4
1.1.9.Потенциальный характер электростатического поля.Работа сил поля при перемещении зарядов. Циркуляция и ротор вектора напряженности
Работа, совершаемая
силами электростатического поля при
перемещении заряда
 на отрезок
на отрезок равна:
равна:
Работа по перемещению единичного положительного заряда численно равна
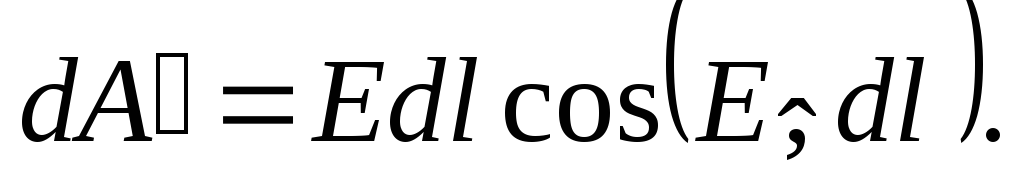
Работа, совершаемая при
перемещении единичного положительного
заряда по конечному пути
 равна
равна
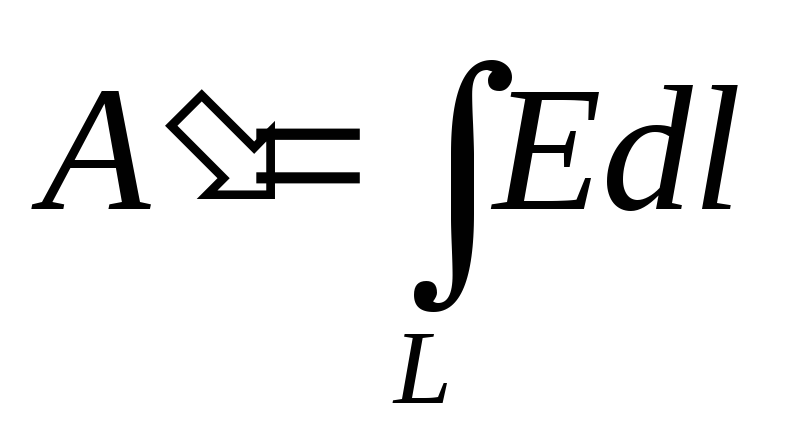 .
(1.1.2)
.
(1.1.2)
Здесь
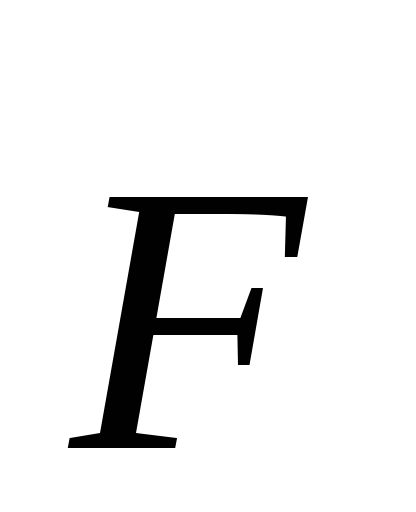 - сила Кулона, которая является центральной
силой. Из механики известно, что поле
центральных сил консервативно.
Следовательно, работа электростатического
поля по перемещению заряда не зависит
от траектории, а определяется только
начальной и конечными ее точками. Работа
по замкнутому пути равна нулю. Поле,
обладающее такими свойствами, называется
потенциальным. Тогда из (1.1.2) имеем:
- сила Кулона, которая является центральной
силой. Из механики известно, что поле
центральных сил консервативно.
Следовательно, работа электростатического
поля по перемещению заряда не зависит
от траектории, а определяется только
начальной и конечными ее точками. Работа
по замкнутому пути равна нулю. Поле,
обладающее такими свойствами, называется
потенциальным. Тогда из (1.1.2) имеем:
 (1.1.3)
(1.1.3)
- циркуляция
вектора
 по замкнутому пути равна нулю.
Поле,
обладающее такими свойствами, называется
потенциальным.
по замкнутому пути равна нулю.
Поле,
обладающее такими свойствами, называется
потенциальным.
Докажем потенциальный характер электростатического поля.
 Рассмотрим
сначала работу электрических сил в поле
элементарного точечного заряда
Рассмотрим
сначала работу электрических сил в поле
элементарного точечного заряда .
Работа этих сил при бесконечно малом
перемещении
.
Работа этих сил при бесконечно малом
перемещении пробного единичного положительного
заряда равна:
пробного единичного положительного
заряда равна:
,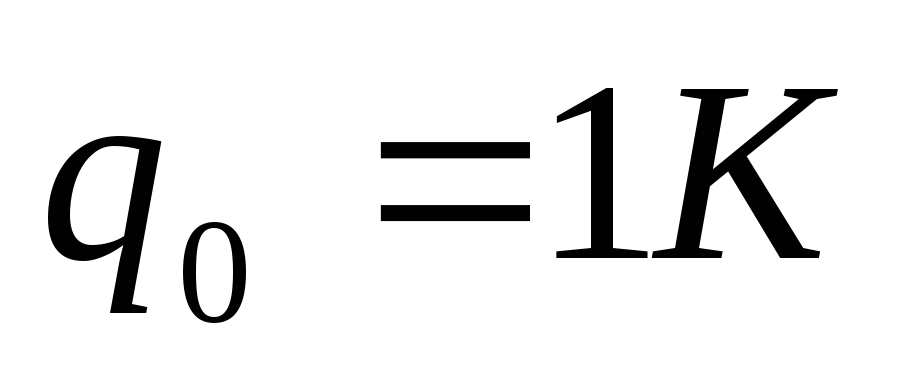
где
 - проекция перемещения пробного заряда
- проекция перемещения пробного заряда на радиус-вектор
на радиус-вектор ,
проведенный из возбуждающего поле
заряда
,
проведенный из возбуждающего поле
заряда .
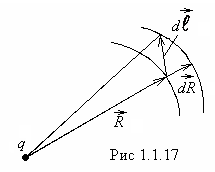
Из рис.1.1.17 видно, что
.
Из рис.1.1.17 видно, что - это приращение
численного значения радиус-вектора
- это приращение
численного значения радиус-вектора ,
то есть увеличение расстояния пробного
заряда
,
то есть увеличение расстояния пробного
заряда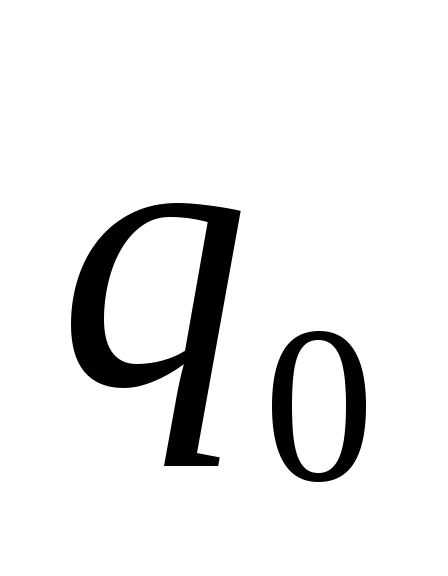 от заряда
от заряда .
Поэтому работа
.
Поэтому работа может быть представлена как полный
дифференциал скалярной функции точки
может быть представлена как полный
дифференциал скалярной функции точки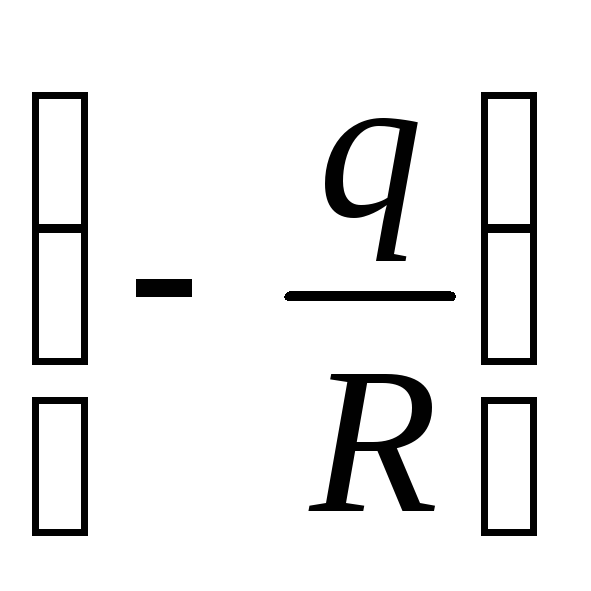 :
:
где
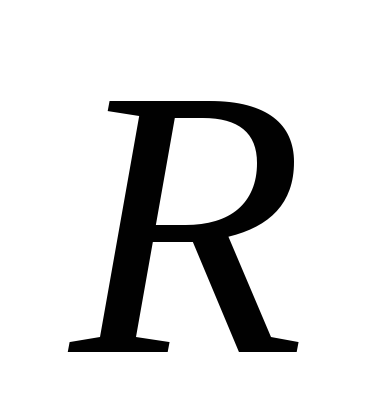 - численное значение радиус-вектора
- численное значение радиус-вектора .
Тогда работа по перемещению единичного
положительного заряда из точки
.
Тогда работа по перемещению единичного
положительного заряда из точки в точку
в точку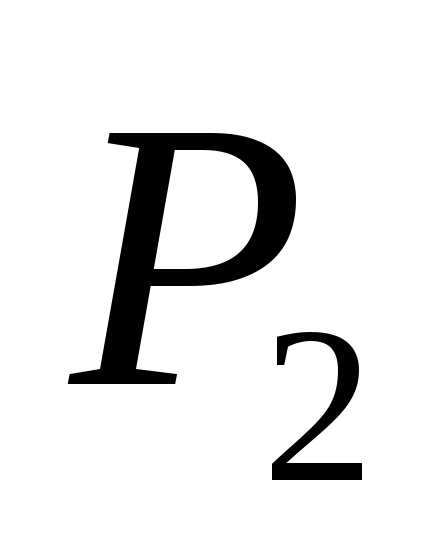 по конечному пути
по конечному пути равна:
равна:
г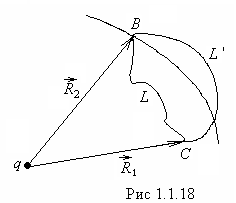 де
де и
и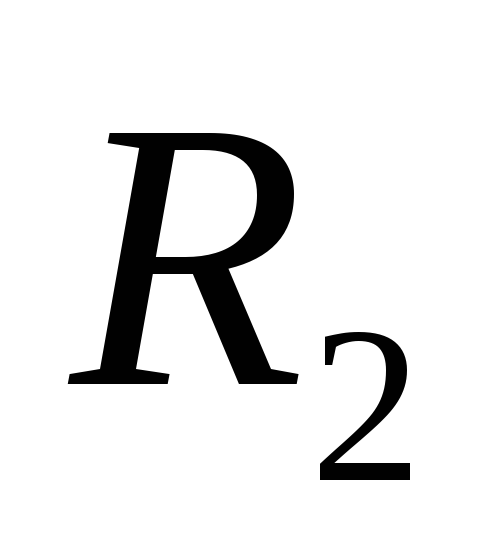 - расстояния начальной и конечной точек
пути от заряда
- расстояния начальной и конечной точек
пути от заряда .
Таким образом, работа электрических
сил на произвольном пути в поле
неподвижного
.
Таким образом, работа электрических
сил на произвольном пути в поле
неподвижного
элементарного точечного заряда
действительно зависит от положений
начальной и конечной точек этого пути
и не зависит от формы пути. На рис.1.1.18
работа на пути
 равна работе на пути
равна работе на пути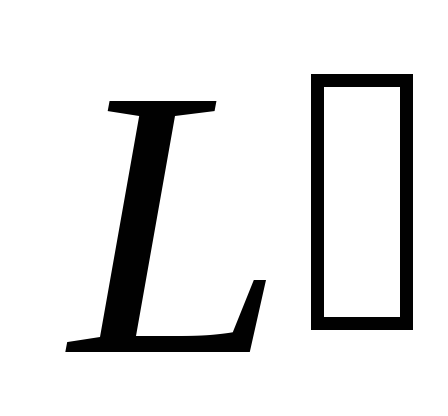 :
избыточная работа, совершаемая на пути
:
избыточная работа, совершаемая на пути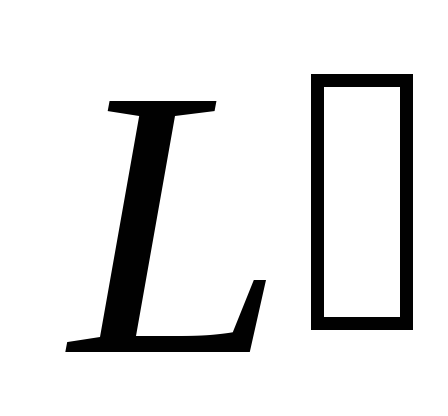 при перемещении пробного заряда за
пределы сферы радиуса
при перемещении пробного заряда за
пределы сферы радиуса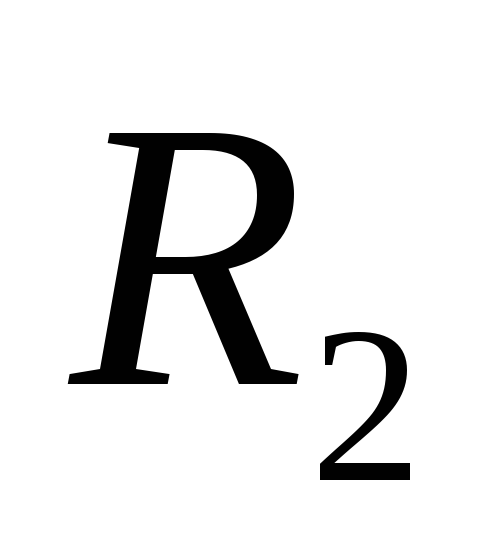 ,
компенсируется отрицательной работой,
совершаемой при последующем приближении
пробного заряда к заряду
,
компенсируется отрицательной работой,
совершаемой при последующем приближении
пробного заряда к заряду на последнем участке пути
на последнем участке пути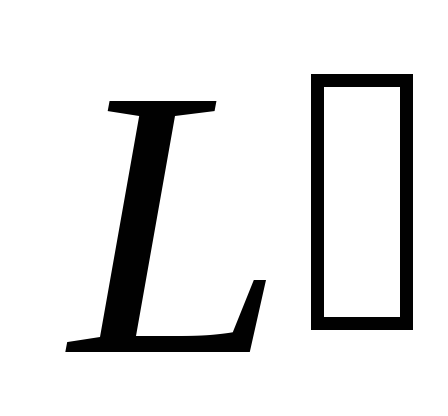 .
Таким образом, поле неподвижного
точечного заряда есть поле потенциальное.
.
Таким образом, поле неподвижного
точечного заряда есть поле потенциальное.
Очевидно, сумма потенциальных полей тоже есть потенциальное поле (так как если работа слагаемых сил не зависит от формы пути, то и работа равнодействующей от нее не зависит). Поле произвольной системы зарядов можно рассматривать как сумму полей каждого из точечных зарядов, поэтому всякое электростатическое поле есть поле потенциальное.
По определению, проекция
 на произвольное направление поля
на произвольное направление поля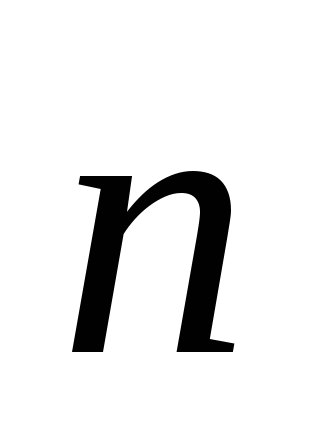 равна
равна
 ,
,
где
 - бесконечно малая площадка, проходящая
через точку
- бесконечно малая площадка, проходящая
через точку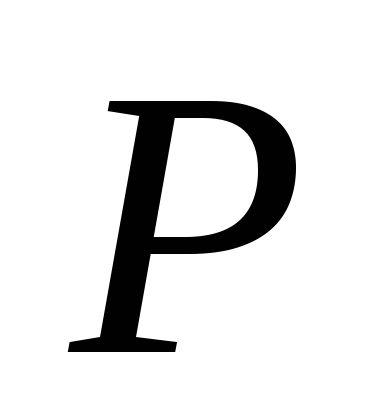 перпендикулярно вектору
перпендикулярно вектору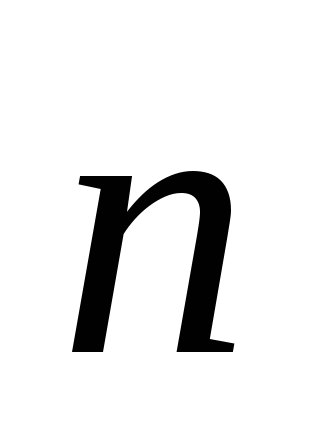 .
.
Так как циркуляция вектора
 по замкнутому контуру равна
по замкнутому контуру равна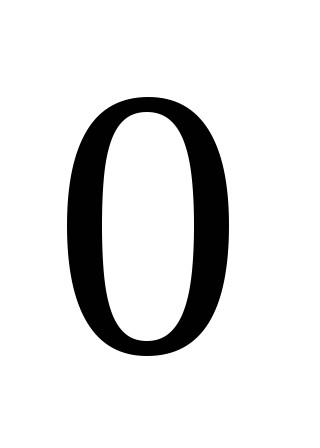 ,
, ,
то
,
то
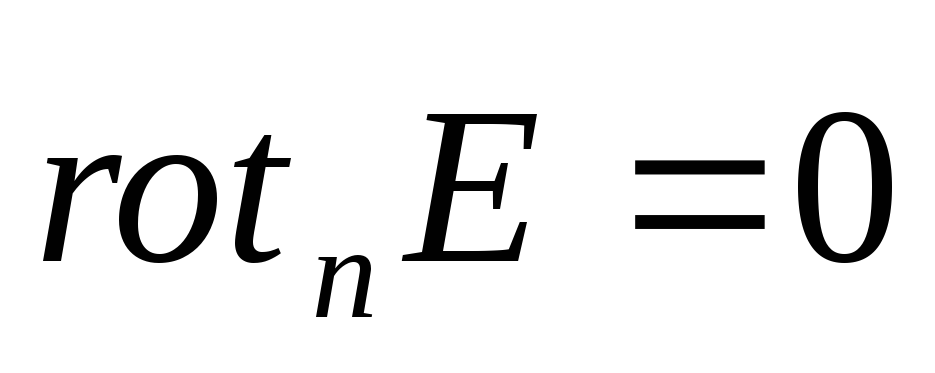 ,
или
,
или .
(1.1.4)
.
(1.1.4)
Так как направление
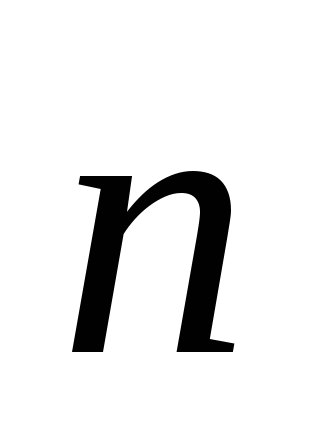 выбрано произвольно, то проекция
выбрано произвольно, то проекция на любые направления равна 0, поэтому
из (1.1.4)
на любые направления равна 0, поэтому
из (1.1.4) во всех точках
электростатического поля, то есть
электростатическое поле является
безвихревым
.
Этот результат можно получить и из
теоремы Стокса. Выражения (1.1.3) и (1.1.4)
эквивалентны.
во всех точках
электростатического поля, то есть
электростатическое поле является
безвихревым
.
Этот результат можно получить и из
теоремы Стокса. Выражения (1.1.3) и (1.1.4)
эквивалентны.


